
Graphically determine the resultant of the following three vector displacements:
- , north of east;
- , east of north; and
- , west of south.
In order to watch this solution you need to have a subscription.
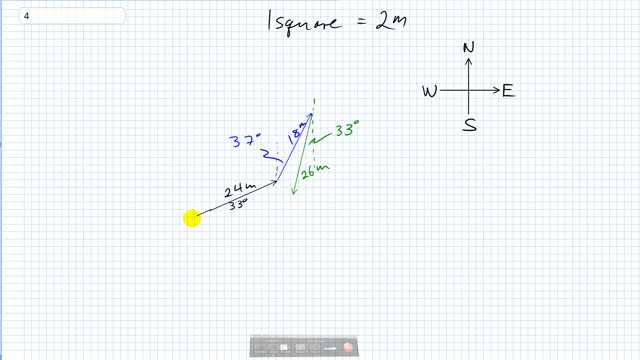
This is Giancoli Answers with Mr. Dychko. The hardest part about this question is understanding what north of east and west of south and those sorts of things mean perhaps when you are drawing all these three vectors. So we'll take one square to be 2 meter say and so here's about 12 squares or so making 24 meters long for the first displacement 33 degrees above east or 33 degrees towards the north of east; north with respect to east could be another way of saying it. And then from that point go further 18 meters 37 degrees east of north so 37 degrees towards the east compared to north and that gives us this blue vector and then go 26 degrees or sorry, 26 meters 33 degrees west of south. So this is 33 degrees compared to south so towards the west of south and the resultant then connects the beginning and the end and so the resultant goes from here to there. And so we roughly, you know, use a ruler or something or count the number of squares here, I guess and figure out the length of this thing so that's 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, I don't know 26 meters or something; I think that an actual calculation would give a fairly significantly different answer because my drawing isn't really that precise. And now to find the angle, we go the inverse tangent of the vertical component divided by the horizontal component so the vertical component looks like it's about 246 so we'll take the inverse tangent of the y—6—divided by the x maybe 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26 meters and then we get, I don't know, 13 degrees. So 26 meters 13 degrees north of east and answers may vary but as long as you understand the process that's the whole idea for graphical solutions.
Hello. Sr. If I decompose in Ax and Ay y got different result can you tell me why. Please.
Hi joeotilio25, this problem is meant to check a students ability to plot vectors on graph paper in the correct direction, and add them together. If you reduced the vectors to components, then added the components together, I would bet that your answer is more precise than mine. If you have an answer that is a some length more than $15 \textrm{ m}$ and less than $30 \textrm{ m}$, then consider your answer correct. I followed the text book instructions to add them graphically, rather than use a calculator. There is a human error in plotting the length and direction for each arrow, and this happens three times, so the errors are compounding. Actually, the error compounds four times when you consider the error in the resultant, so don't be surprised of your answer differs from what's shown. The thing to learn from this video is how to plot vectors, and what it means, graphically speaking, to add three of them together.
Hello, I got a different answer for this question. I divided all the vectors into x and y components and used pythagorean theorem at the end to find the resultant vector. My answer is 22.53 km ( 22.53 degrees North of East ).
Hi chaegyunkang, that's a fair question that other's have had as well. I'll paste my response to another student's similar point: "this problem is meant to check a students ability to plot vectors on graph paper in the correct direction, and add them together. If you reduced the vectors to components, then added the components together, I would bet that your answer is more precise than mine. If you have an answer that is a some length more than 15 m and less than 30 m, then consider your answer correct. I followed the text book instructions to add them graphically, rather than use a calculator. There is a human error in plotting the length and direction for each arrow, and this happens three times, so the errors are compounding. Actually, the error compounds four times when you consider the error in the resultant, so don't be surprised of your answer differs from what's shown. The thing to learn from this video is how to plot vectors, and what it means, graphically speaking, to add three of them together."
All the best,
Mr. Dychko
This seemed to be completely off from what I got. I understand it is an estimation, but the correct answers were off by a lot.
Hi bmalan, what answer did you get? "completely off" might mean there's enough difference that an error occurred, or maybe it just means "different, but agree within expected error of the graphical technique". It's hard to know without knowing your answer.