Your Textbook EditionPricingAbout UsFeaturesReviewsFAQContact
Get startedLog in
Giancoli 7th Edition textbook cover
Giancoli's Physics: Principles with Applications, 7th Edition
3
Kinematics in Two Dimensions; Vectors
Change chapter
3-2 to 3-4: Vector Addition
1
play arrow4:22
2
play arrow1:19
3
play arrow1:50
4
play arrow2:19
5
play arrow1:52
6
play arrow3:07
7
play arrow2:05
8
play arrow1:48
9
play arrow3:00
10
play arrow5:06
11
play arrow3:02
12
play arrow5:42
13
play arrow7:07
14
play arrow2:30
15
play arrow2:38
16
play arrow2:53
3-5 and 3-6: Projectile Motion
17
play arrow1:33
18
play arrow0:59
19
play arrow1:56
20
play arrow2:31
21
play arrow1:52
22
play arrow2:00
23
play arrow4:10
24
play arrow3:43
25
play arrow1:22
26
play arrow2:35
27
play arrow5:12
28
play arrow3:03
29
play arrow4:07
30
play arrow4:42
31
play arrow1:47
32
play arrow4:10
33
play arrow7:46
34
play arrow3:38
35
play arrow6:53
36
play arrow5:25
37
play arrow6:40
3-8: Relative Velocity
38
play arrow2:09
39
play arrow2:31
40
play arrow1:03
41
play arrow2:43
42
play arrow2:38
43
play arrow2:37
44
play arrow6:37
45
play arrow1:46
46
play arrow2:24
47
play arrow1:48
48
play arrow4:54
49
play arrow1:29
50
play arrow2:27
51
play arrow4:22
Question by Giancoli, Douglas C., Physics: Principles with Applications, 7th Ed., ©2014, Reprinted by permission of Pearson Education Inc., New York.
Problem 13
Q

For the vectors given in Fig. 3-35, determine

  1. A⃗−B⃗+C⃗\vec{A} - \vec{B} + \vec{C},
  2. A⃗+B⃗−C⃗\vec{A} + \vec{B} - \vec{C}, and
  3. C⃗−A⃗−B⃗\vec{C} - \vec{A} - \vec{B}.
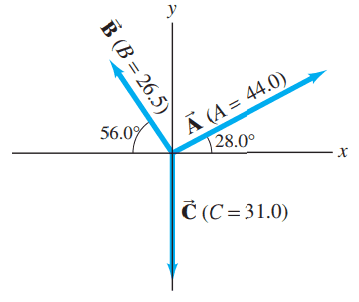
Problems 9, 10, 11, 12, and 13. Vector magnitudes are given in arbitrary units.
Figure 3-35 Vector magnitudes are given in arbitrary units.
A
  1. 62.6 units, 31.1∘ below the pos. x-axis62.6\textrm{ units, } 31.1^\circ \textrm{ below the pos. x-axis}
  2. 77.4 units, 71.9∘ above pos. x-axis77.4\textrm{ units, }71.9^\circ \textrm{ above pos. x-axis}
  3. 77.4 units, 71.0∘ below neg. x-axis77.4\textrm{ units, }71.0^\circ \textrm{ below neg. x-axis}
Giancoli 7th Edition, Chapter 3, Problem 13 solution video poster
Padlock

In order to watch this solution you need to have a subscription.

Get Started
View sample solution

|

Log in
VIDEO TRANSCRIPT

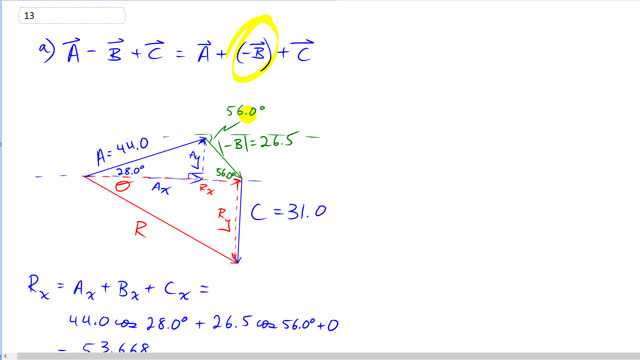
This is Giancoli Answers with Mr. Dychko. Vector A is 44 units long and 28 degrees above the positive x-axis; vector negative B is 56 degrees below the positive x-axis means down to the right and has a length of 26.5— that's what these vertical lines here are it's absolute value which means length of vector— and vector C is 31 units down so we are using the head to tail method and then putting the tail of negative B on the head of vector A because I'm using considering it all an addition problem— addition, addition— and instead of minus B, I'm putting a vector plus negative B and so flipping vector B around compared to what it normally is. And then the resultant goes from the very beginning to the very end and it has a x-component which is the x-component of A plus the x-component of this negative B and the resultant has a y-component of vector A and then B and then C all added together; okay, let's see what that looks like. So for x-component of the resultant, we have x-component of A which is 44 times cos of 28 so that A x in blue goes from here to here and that's added to 26.5—length of vector B— times cos of 56 so cos of 56 gives you this part that's right here which is the same as this part down here for x-component of B— both of those to the right, both of those are positive— and then C has no x-component so it's just zero and we have 53.668 x-component of the resultant. And then the y-component is upwards so positive 44.0—length of A— times sin 28 so that gives us this part here minus 26.5 times sin of 56 gives us the x-component of B which is this part here that's B y or sorry this is the x-component, y-component is what I meant and then we have minus 31 which is the length of C and both of the parts that are down—B y and C y—end up being negative and so we have negative 32.313 is the y-component of the resultant; add them together with Pythagoras so take the square root of the sum of the squares and you get 62.645. And then inverse tangent of the y-component divided by the x-component of the resultant gives us the angle Θ below the positive x-axis. So that's 62.6 units, 31.1 degrees below the positive x-axis is the resultant of A minus B plus C. For part (b), the picture looks like this where you have vector A again and then plus B plus the opposite of C so opposite of C is upwards, 31 units, and the resultant goes from the very beginning to the very end and it's the same process to figure it out; we have the x-component of A plus the x-component of B and plus x-component of C. X-component of B is negative because it's to the left here— it's this little blue part here from here to here— and we find that by going 26.5 times cos 56 and it's minus 26 because it's to the left; the x-component of A is 44.0 times cos 28 so that takes us from here to here, that's the x-component of A along this part here and C has no x-component, we have 24.031 x-component of resultant. Y-component is the y-component of A which is upwards and it's 44 times sin 28—sin because it's the opposite— and then plus 26.5—length of B— times sin 56 and then plus 31—the length of C— and that gives 73.626 take the square root of the sum of the squares and then take the inverse tangent of the y-component of the resultant divided by the x-component of the resultant and we get 77.4 units, 71.9 degrees above the x-axis. Then in part (c), the picture is like this where you have C which is straight down plus negative A so put the tail of negative A on the head of vector C and so that takes us down there and then plus the opposite of vector B and here's the opposite of vector B we'll put the tail of negative B on the head of negative A and then the resultant goes from the very beginning to the very end like this; always good to draw a picture when you are dealing with vectors like this especially because it helps you figure out how to calculate your angle and what your angle is with respect to and in this case, it will be below the negative x-axis. So we have x-component of A is negative 44 times cos 28 —negative because it's to the left— and then plus 26.5 times cos 56 and this is positive because this x-component of B which is just this little bit here lining up with the head of vector B there that little bit is to the right so it's positive and then we have no x-component for C and so we end up with negative 24.031 x-component for the resultant and then for the y, we have y-component of A which is 44 times sin 28 and that's negative because it's downwards and this is what we are calculating here this little bit which is the same as this little bit and that's sin 28 because this is the opposite and then times by the length of A—44— and negative because it's downwards and then minus 26.5 times sin 56 for the y-component of B and then minus 31—y-component of C— and straight down so there's no trick needed. And then take the square root of sum of the squares to get the resultant length and then inverse tangent of the y-component of the resultant divided by the x-component of the resultant and based on the picture, we know that this is below the negative x-axis. So there we have it, 77.4 units, 71.9 degrees below the negative x-axis for part (c).

COMMENTS
By sophiaswimgirl on Sat, 1/21/2017 - 1:16 AM

In part a) I'm confused as to why By is negative.
sin 56 = By/(-26.5) will result in a negative - I get that - but in question number 9, which uses the same vectors, the solution to By was positive, so why aren't they the same?

Is it because in the equation we're asked to solve for, we have to subtract vector B? Then why isn't Bx negative?

Thank you.

By Mr. Dychko on Sun, 2/5/2017 - 9:19 PM

Hi sophiaswimgirl,

In question 13 the vector B is the negative of what it was in problem #9, which makes it point in the opposite direction. When I see a vector being subtracted, as vector B is in this case, I like to think of it as 'adding it's negative', which mean apply the usual rules for adding vectors, but flip around the one that's being subtracted. Instead of up and to the left in #9, it is now down and to the right here in #13. Since it's pointing downish, that makes the y-component, ByB_y, negative.

In both cases, the calculation for ByB_y was 26.5sin⁡(56∘)26.5 \sin(56^\circ) but here in #13 the result gets a negative in front if it despite the calculator saying 'positive'. This has to do with our understanding of the physical situation, in that the vector is pointing down, and so with that understanding we just put the negative there, regardless of what the calculator says. This might be going on a tangent, but just for arguments sake, if you wanted to always have the calculator say the correct sign, you would have to enter angles in standard position which is measured counter clockwise starting from the positive x-axis. In problem 13 the standard position angle of vector B is 360−56=304∘360 - 56 = 304^\circ, in which case 26.5×sin⁡(304∘)=−21.97...26.5 \times \sin(304^\circ) = -21.97... with the negative sign, rather than 26.5×sin⁡(124∘)=+21.97...26.5 \times \sin(124^\circ) = +21.97... (where 124∘124^\circ is the standard position angle in #9). I don't recommend changing your angles to standard position, but I just mention it so that you're more comfortable placing negative signs where they belong 'by decrie', secure in knowing that there is a way to make the mathematics consistent with the physical reality if you felt like it. You're not doing anything wrong, in other words, by overriding the sign of what the calculator says and choosing the sign that fits the physical situation.

Maybe that was a bit long, but I hope it helps.

All the best,
Mr. Dychko

By jxmiller9975 on Thu, 1/27/2022 - 8:00 PM

Hello,
How do you know when the angle is "below the + x-axis" or "above the - x-axis" etc. Is there a way to know that without visualizing it graphically?

By jxmiller9975 on Thu, 1/27/2022 - 8:00 PM

Hello,
How do you know when the angle is "below the + x-axis" or "above the - x-axis" etc. Is there a way to know that without visualizing it graphically?

Privacy policyTerms of serviceHelp center

Find us on:

Facebook iconTrustpilot icon
Giancoli Answers, including solutions and videos, is copyright © 2009-2024 Shaun Dychko, Vancouver, BC, Canada. Giancoli Answers is not affiliated with the textbook publisher. Book covers, titles, and author names appear for reference purposes only and are the property of their respective owners. Giancoli Answers is your best source for the 7th and 6th edition Giancoli physics solutions.