GiancoliAnswers

You are here

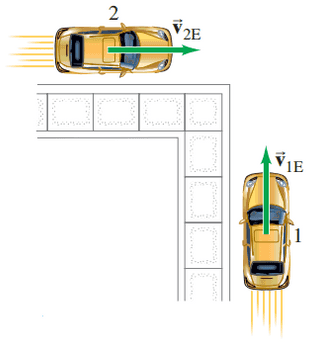
  4. Problem 51
Select a problem
Question: 

Two cars approach a street corner at right angles to each other (Fig. 3-47). Car 1 travels at a speed relative to Earth $v_\textrm{1E} = 35 \textrm{ km/h}$, and car 2 at $v_\textrm{2E} = 55 \textrm{ km/h}$. What is the relative velocity of car 1 as seen by car 2? What is the velocity of car 2 relative to car 1?

Problem 51.

Figure 3-47.

Source: Giancoli, Douglas C., Physics: Principles with Applications, 7th Edition, 2014.

Quick Answer: 

$v_{12} = 65\textrm{ km/h, } 58^\circ \textrm{ West of North. } $$v_{21} = 65\textrm{ km/h, }32^\circ \textrm{ South of East}$

Giancoli 7th Edition, Chapter 3, Problem 51

(4:22)

Chapter 3, Problem 51 is solved.

View sample solution

Transcript for this Giancoli solution

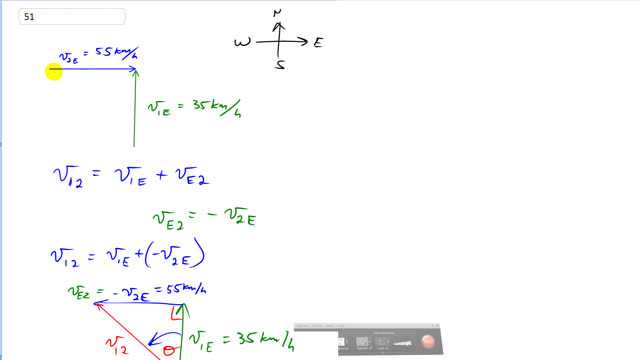
This is Giancoli Answers with Mr. Dychko. Car 1 is approaching this intersection going north at 35 kilometers an hour and car 2 has a velocity with respect to the Earth of 55 kilometers an hour traveling straight east and the question is what is the velocity of car 1 as seen by somebody in car 2? And that's gonna be the velocity of car 1 with respect to the Earth plus the velocity of the Earth with respect to car 2 which is an unusual way of talking about this velocity. Notice that it's v E2 instead of v 2E so we put velocity of the object first and then the reference frame is the second subscript and we are doing that because we want these inner subscripts to be the same and then in which case they cancel leaving us with velocity of these outer subscripts; 1 with respect to 2 which is what we want. So to figure out this velocity of the Earth with respect to car 2 which would be you know, if you are somebody in car 2 and you are just looking at the ground this is what you would see, you'd see the Earth traveling under you to the left and that would be the velocity of the Earth in the reference frame of the car. So the Earth is passing by beneath you and it's the negative of the velocity of car 2 with respect to the Earth so you can always switch the subscripts around by just putting a negative sign in front and that will flip the vector around so that it's pointing in the opposite direction. So v 12 equals v 1E plus the negative of v 2E and so v E2 is the negative of v 2E which is 55 kilometers an hour going to the left. And so we have this right triangle to consider and we'll figure out the length of this hypotenuse which is the magnitude of our velocity and then we'll also figure out angle Θ. So v 12 is this square root of 35 kilometers an hour squared plus 55 kilometers an hour squared which gives 65 kilometers an hour and the angle is gonna be the inverse tangent of 55 over 35 and that's 58 degrees towards the west of north so this is a velocity of car 1 as seen by somebody in car 2. And then we do the opposite and figure out the velocity of car 2 by somebody sitting in car 1. And we'll then say that v 21 equals v 2E—velocity of car 2 with respect to the Earth—plus velocity of the Earth with respect to car 1 and this is the negative of velocity of car 1 with respect to the Earth and so we flip around the 1E and have it point down instead of up and here's v 2E straight to the right and it's the same triangle just they are pointing in different directions and so we have that the length of the hypotenuse is the same so 65 kilometers per hour and the angle we wanted to specify now though was this one and that's gonna be well, this is a right triangle so the total of all three angles has to be 180 and there's 90 accounted for here which leaves 90 to share between these two angles this one down here—this γ—we have already figured out that's this angle here which I call Θ up there and that's 58 degrees and so the angle Θ we want in this question is gonna be 90 minus the 58 degrees which is 32 degrees, that's towards the south of east. So the velocity of car 2 as seen by somebody in car 1 is 65 kilometers an hour, 32 degrees south of east.