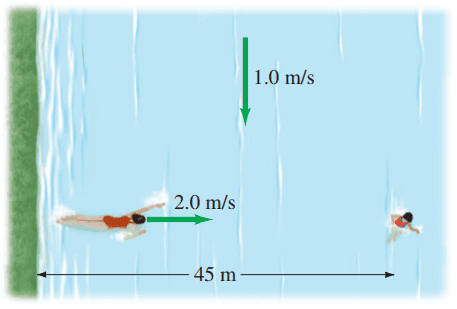
A child, who is 45 m from the bank of a river, is being carried helplessly downstream by the river's swift current of 1.0 m/s. As the child passes a lifeguard on the river's bank, the lifeguard starts swimming in a straight line (Fig. 3-46) until she reaches the child at a point downstream. If the lifeguard can swim at a speed of 2.0 m/s relative to the water, how long does it take her to reach the child? How far downstream does the lifeguard intercept the child?

In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. The lifeguard is swimming out towards the child at just the moment when the child passes the lifeguard and so the lifeguard doesn't need to have any vertical component or upstream or downstream component to their velocity because they just need to go straight horizontal and they are gonna get carried downstream, sure enough, but at the same rate that the child is so the lifeguard then just has to swim straight horizontal. And so to close this horizontal gap of 45 meters, to figure out the time that it will take we know that the distance 45 meters equals the x-component of the velocity times time but that x-component of the velocity is entirely the lifeguard with respect to the water's velocity. So we'll divide both sides by v x here and so that's d x divided by velocity of the lifeguard with respect to the water which is 45 meters divided by 2 meters per second which is 23 seconds to reach the child. And then how far downstream will they will lifeguard go before reaching the child? Well, we know that the y-component of the velocity of the lifeguard will be the velocity of the water with respect to the shore which is 1 meters per second multiplied by this time of 22.5 seconds gives about 23 meters downstream when the lifeguard reaches the child.
