
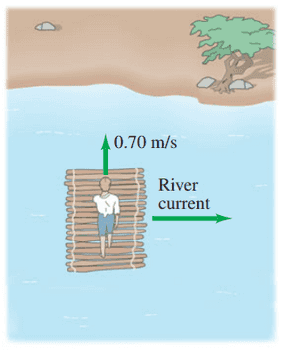
Huck Finn walks at a speed of 0.70 m/s across his raft (that is, he walks perpendicular to the raft's motion relative to the shore). The heavy raft is traveling down the Mississippi River at a speed of 1.50 m/s relative to the river bank (Fig. 3-42). What is Huck's velocity (speed and direction) relative to the river bank?
Note: technically a better answer is since the textbook asks for the answer "relative to the river bank". Please see the comment below for more details.
In order to watch this solution you need to have a subscription.
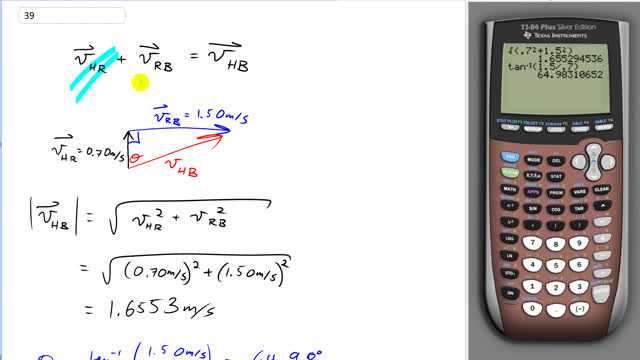
This is Giancoli Answers with Mr. Dychko. We want to know the velocity of Huck Finn with respect to the river bank so we need to add the velocity of Huck Finn with respect to the river plus the velocity of the river with respect to the bank and the inner subscript's are the same here, they are both R—river—and so they disappear and we are left with H and B in our answer; Huck Finn with respect to the bank which is what we want. And so we have the two vectors here that we know; one is Huck Finn with respect to the raft— 0.7 meters per second straight across the river— and then we know the velocity of the river with respect to the bank which is 1.5 meters per second downstream and this red vector is the resultant; this is the velocity of Huck Finn with respect to the river bank. So the speed or the magnitude of the velocity is the square root of the sum of the squares of these two velocities here so that's the square root of 0.7 meters per second squared plus 1.5 meters per second squared that gives 1.6553 meters per second so that's the magnitude of the velocity. And then the direction let's say we have Θ in here between the resultant and straight across that would make tan that angle would be the opposite over the adjacent and then the angle then is the inverse tangent of that opposite 1.5 meters per second divided by the adjacent which is 0.7 meters per second which is about 65 degrees and you have to specify what you are measuring your angle with respect to because it's equally valid I mean it's always valid to measure your angle with respect to whatever you like but I could imagine somebody could also put an angle here with respect to the river bank and that would be the complement of this angle 25 degrees but what we have chosen to do here is 65 degrees with respect to straight across. So our answer is velocity of Huck Finn with respect to the bank is 1.66 meters per second, 65 degrees downstream from straight across. And I have to say downstream because well, if I just say 65 degrees, this would also be 65 degrees here and so I have to say downstream whereas this would be 65 degrees upstream.
In the back of the book it says 25 degrees. I got the same answer as you when I tried it on my own before looking at your video. Is that a mistake the book made?
Hi p.zeppelin, thanks for the question. I just re-read the question in the textbook, and the wording is to give the angle "relative to the river bank", in which case the book is correct in saying . We both found answers relative to "straight across". I would say that if we are explicit about our choice of reference then our answer is fine, but I suppose the better answer is . I'll make a note above in the quick answer. Just to make it clear, and as a way of checking our conclusion, notice that our answer and textbook's answer are complementary (add to 90): , which is expected since the angle between the river bank and straight across is .
Cheers,
Mr. Dychko