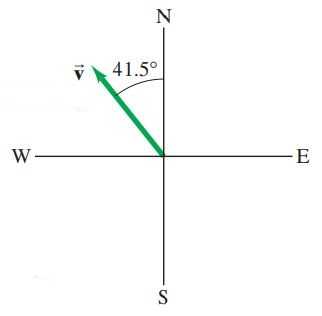
An airplane is traveling 835 km/h in a direction $41.5^\circ$ west of north (Fig. 3-34).

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. So the airplane travels 835 kilometers 41.5 degrees to the west of north and the components are gonna be well, for the x-component it's gonna be 835 times sin of 41.5 because the x-component is the opposite leg of this right triangle compared to this angle 41.5. And so, you know, sin Θ is opposite over hypotenuse and so we'll multiply both sides by the hypotenuse and we get that v x is v times sin Θ. So we have 487.03 is our answer to that and then we do the same sort of story for the y-component which we'll use cosine for in this case and so we have 835 times cos 41.5 giving us —these numbers are from an old addition by the way, get rid of that— gives us 625 kilometers per hour north. And it's 553 kilometers per hour west for the x-component. Okie-dokie. For part (b), the distance in the x-direction is gonna be the x-component of the velocity times 1.75 hours which gives 968 kilometers to the west. And then for the y-component we have the y-component of the velocity 625.38 times 1.75 hours which is 1090 with three significant figures; 1090 kilometers to the north.