
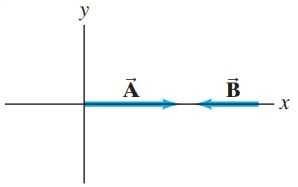
Figure 3-33 shows two vectors, and , whose magnitudes are and . Determine if
- ,
- ,
- . Give the magnitude and direction for each.

In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. So here we have vector A 6.8 units to the right and vector B 5.5 units to the left. So we are taking the right to be positive so here's the picture for when we have finding vector C which is vector A plus B; it's the head to tail method so we put the tail of the second vector on the head of the first vector and then the resultant goes from the starting point, the tail of the first vector to the head of the last vector so that C is in red there. So that's 6.8 to the right minus 5.5 to the left which is 1.3 units and since we have defined the right direction to be positive, this also states the direction so 1.3 positive means to the right and the positive x-direction. Part (b) we have vector A minus vector B and when dealing with subtracting vectors, I like to think of it as adding the opposite vector and the opposite means you flip the direction around So negative B is gonna be the same as vector B but pointing to the right now instead of to the left and we have then using the head to tail method, we put the tail of this negative B on the head of vector A and we get the resultant is starting from the very beginning to the very end, there and it's 6.8 units minus negative 5.5 which gives us 12.3 units. And for the last question, we have B in the first vector, in this case, and then minus A which is plus the opposite of A plus A in the other direction to the left now and our resultant is this then. And so that's the negative 5.5 minus 6.8 for a total of negative 12.3 units so that's 12.3 to the left.
Can y explain the part B and B because I don't understand why change the direction. Please.
Hi joseotilio25, this is a personal preference. I choose to make every vector subtraction problem an addition problem. When subtraction comes along, as in part b) here, I choose to make it an addition problem by adding the second vector in the opposite direction. This technique has the advantage that every vector problem, including subtraction, involves putting the tail of the second vector on the head of the first. To illustrate why this works, consider . This can also be written as an addition problem by adding the opposite of the second number. The second number is , so adding it's opposite means adding . It looks like . It works out to the same answer, as it should, and with arithmetic there's no advantage to making subtraction into an "adding the opposite" question, whereas with vectors, changing subtraction to "adding the opposite" has the advantage that you can keep on using the "head to tail" method. In the end, it's an issue of personal preference. You could instead learn a "head to head" method, and create the resultant by connecting the remaining tails if you want a different technique.
what about the last part of the problem that asked to find the magnitude and direction ?
Hi samkvertus, thanks for the question. Both the magnitude and directly are actually given here. Direction in this case is "to the left" when the resultant is negative, whereas it's "to the right" when positive. The magnitude is the number when ignoring the negative sign. This is explained more in the video, so consider giving it a second view.
All the best,
Mr. Dychko