
Super Invar, an alloy of iron and nickel, is a strong material with a very low coefficient of thermal expansion . A 1.8-m-long tabletop made of this alloy is used for sensitive laser measurements where extremely high tolerances are required. How much will this alloy table expand along its length if the temperature increases ? Compare to tabletops made of steel.
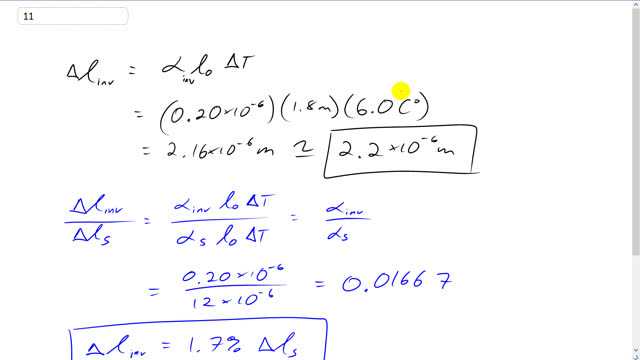
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. The amount that the 1.8 meter table made of super invar will expand equals the coefficient of linear expansion for a super invar of 0.2 times 10 to the minus 6 times 1.8 meters times the 6 Celsius degrees temperature change, and that's 2.2 times 10 to the minus 6 meters which is very small, 2.2 micrometers. The ratio of change in length of the super invar table versus the change in length of a steel table is coefficient of linear expansion for invar times l naught times Δt divided by coefficient of linear expansion for steel times the same l naught times Δt. So, these things cancel meaning ratio and length changes will be the ratio in the coefficients of linear expansion. So, that's 0.2 times 10 to the minus 6 divided by 12 times 10 to the minus 6 which is 0.01667 and multiply that by 100% and you get this. So, the change in length for the super invar table will be about 1.7% the change in length that would happen with a steel table.