The lowest pressure attainable using the best available vacuum techniques is about $10^{-12} \textrm{ N/m}^2$. At such a pressure, how many molecules are there per $\textrm{cm}^3$ at $0 ^\circ \textrm{C}$?

VIDEO TRANSCRIPT

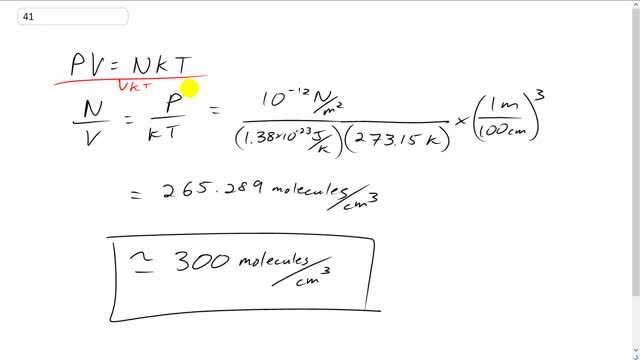
This is Giancoli Answers with Mr. Dychko. P V equals the number of molecules times Boltzmann constant times temperature and we can solve this for N over V by dividing both sides by V K and T. So, we have pressure over K T because the v's cancel, equals the number of molecules divided by the volume and because the K T cancels here. And that's 10 to the minus 12 newtons per meter squared lowest attainable pressure, and then divided by Boltzmann constant 1.38 times 10 to the minus 23 joules per kelvin times the standard temperature of 273.15 kelvin. And this is going to give us number of molecules per cubic meter, and so we have to convert that into per cubic centimeter, because that's what the question asks us for, by multiplying by 1 meter for every 100 centimeters, cubed, and we end up with about 300 molecules per cubic centimeter.