An ordinary glass is filled to the brim with 450.0 mL of water at $100.0 ^\circ \textrm{C}$. If the temperature of glass and water is decreased to $20.0 ^\circ \textrm{C}$, how much water could be added to the glass?

VIDEO TRANSCRIPT

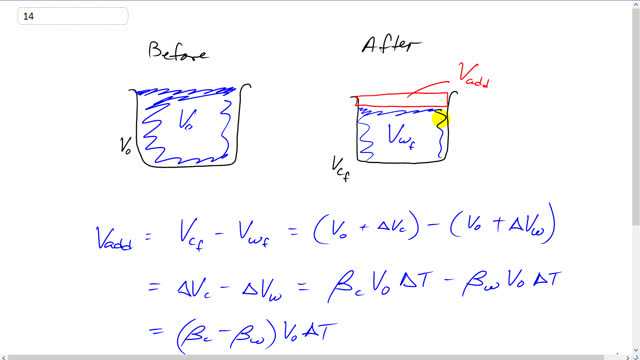
This is Giancoli Answers with Mr. Dychko. When this container full of water cools down, both, the container and the water will reduce their volumes as a result of this decrease in temperature. And so the amount of water we can add is going to be the amount by which the water contracts more than the container. So, the amount we can add is going to be the final container volume minus the final water volume. And they both start out with the same initial volume because the container is completely full of the water. So, v naught over v initial for the water and the container are both the same. So, the final container volume will be the initial container volume, v naught, plus the change in the volume of the container and then minus the initial volume of the water plus the change in the volume of the water. And these v naughts are both the same to begin with and so they make 0. And we have that the volume we can add is the difference in the change in volumes of the container in water. So, here is the change in volume of the container, the coefficient of volume expansion of the ordinary glass times its initial volume times the change in temperature and then minus the change in volume of the water coefficient of volume expansion for water times v naught Δt. And v naught Δt are the same, we can factor it out and so we have β c minus β w times v naught Δt. And the coefficient of volume expansion for glass is 27 times 10 to the minus 6 minus the coefficient of volume expansion for water, 210 times 10 to the minus 6. And we can see that the volume of the water is going to decrease more than the volume of the glass, and we can see that based on knowing that the coefficient of volume expansion for water is so much greater. This means that the water volume is more sensitive to changes in temperature because this is a greater coefficient. So, we'll take this difference and multiply it by the original volume of 450.0 milliliters times the final temperature of 200.0 degrees Celsius minus the initial temperature of 100 and that gives about 6.59 milliliters is the amount of additional water we can add, this is the amount by which the water volume decreases more than the container volume.