A certain car has 14.0 L of liquid coolant circulating at a temperature of $93 ^\circ \textrm{C}$ through the engine’s cooling system. Assume that, in this normal condition, the coolant completely fills the 3.5-L volume of the aluminum radiator and the 10.5-L internal cavities within the aluminum engine. When a car overheats, the radiator, engine, and coolant expand and a small reservoir connected to the radiator catches any resultant coolant overflow. Estimate how much coolant overflows to the reservoir if the system goes from $93 ^\circ \textrm{C}$ to $105 ^\circ \textrm{C}$. Model the radiator and engine as hollow shells of aluminum. The coefficient of volume expansion for coolant is $\beta = 410 \times 10^{-6} /\textrm{C}^\circ$.

VIDEO TRANSCRIPT

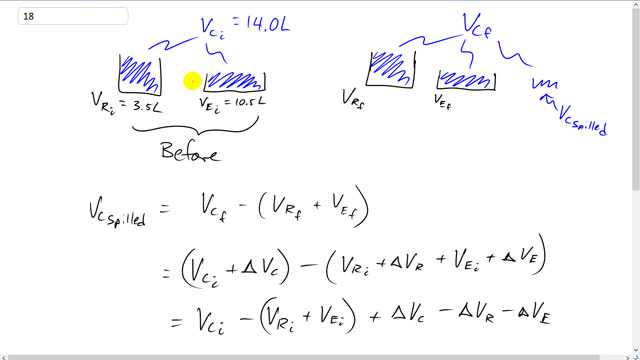
This is Giancoli Answers with Mr. Dychko. We start off with some coolant, entirely filling the radiator and the engine block. And at this initial temperature the total volume of coolant equals the total volume of the radiator plus the volume of the engine. And then after things are heated up a bit. This is the after picture we have total volume of the coolant is going to be in the... It's going to be the final volume of the radiator plus the final volume of the engine plus some volume that's in the overflow, some volume of coolant that spills out of this radiator engine system. And this is normal, supposed to go into this overflow thing, and then it gets sucked back in once the engine cools back down. So, the amount that spilled over, though, into the overflow is going to be the final volume of the coolant, that's the total final volume the spill plus the parts contained within this and this minus the volumes of the final volumes of the radiator plus the volume of the engine. So, the final volume of the coolant is the coolant initial volume plus its change in volume. And we're gonna go minus the radiator's initial volume plus its change in volume plus the engine's initial volume plus the engine's change in volume. And we can... We have vci minus this plus this. But the initial volume of the coolant equals the initial volume of the radiator plus the engine so, this bracket is equal to this and so these things make 0. And we're left with the change in volume of the coolant minus the change of volume of the radiator minus the change of volume of the engine. And so we can substitute for each of these things. We have the coefficient of volume expansion for the coolant times the coolant initial volume times Δt minus the coefficient of volume expansion for aluminum times the volume initial volume of the radiator fans times the same change in temperature. The radiator and the engine, they're both made out of aluminum were told. So, we do the same thing to this engine term. And we can factor out the Δt. I can also factor out the β aluminum but I didn't bother. So, we have 105 degrees Celsius final temperature minus 93 degrees Celsius initial temperature times 410 times 10 to the minus 6 volume expansion coefficient for the coolant times the coolant's initial volume of 14.0 liters minus 75 times 10 to the minus 6 volume expansion coefficient for aluminium times the radiator's initial volume of 3.5 liters minus 75 times 10 to the minus 6 times 10.5 liters for the initial volume of the engine. And this works out to 0.05628 liters which is 56 milliliters. And that's the amount of coolant that will go into the overflow once the engine heats up a bit.