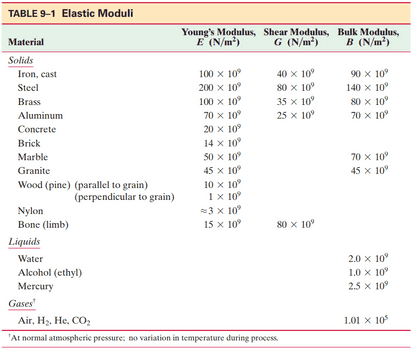
An aluminum bar has the desired length when at $12 ^\circ \textrm{C}$. How much stress is required to keep it at this length if the temperature increases to $35 ^\circ \textrm{C}$? [See Table 9–1.]

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. As a result of thermal expansion the change in length of this aluminum rod will be the equal to the coefficient of linear expansion times the rod's initial length times has change in temperature. Now, the elastic modulus, if you look back at chapter 9, equals stress divided by strain. And we can solve this for stress by multiplying both sides by strain which makes stress equal to elastic modulus times strain. And the connection between this stuff in blue and the stuff in this chapter with thermal expansion is the strain is change in length divided by initial length and we have a formula for change in length as a result of change in temperature here. So, we substitute this in for Δl so, stress is elastic modulus times α li Δt over li. And the li’s cancel, meaning that stress is the elastic modulus times the coefficient of linear expansion times the change in temperature. Turns out it doesn't matter what the initial temperature is. Or, sorry, the initial length I should say. So, that's 70 times 10 to the 9 newtons per square meter elastic modulus for this material times 25 times 10 to the minus 6 coefficient of linear expansion for aluminum times 35 degrees Celsius minus 12 degrees Celsius. And that gives about 4.0 times 10 to the 7 newtons per square meter of stress in order to keep this thing at the same length. Because this rod is going to have some, you know, it's going to be, this is the increase in length as a result of the expansion. And then this is the decrease in length as a result of some stress that's squishing it together. So, they're equal magnitudes even though one's an expansion, the other one's a compression.