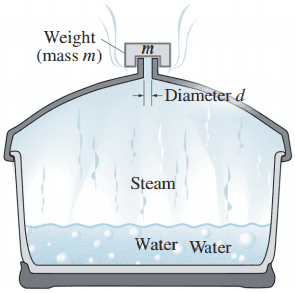
A pressure cooker is a sealed pot designed to cook food with the steam produced by boiling water somewhat above $100 ^\circ \textrm{C}$. The pressure cooker in Fig. 13–32 uses a weight of mass $m$ to allow steam to escape at a certain pressure through a small hole (diameter $d$) in the cooker’s lid. If d = 3.0 mm, what should $m$ be in order to cook food at $120 ^\circ \textrm{C}$? Assume that atmospheric pressure outside the cooker is $1.10 \times 10^5 \textrm{ Pa}$.

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. So, we want the water in this pressure cooker to boil at 12 degrees Celsius and that'll happen when the pressure inside equals the saturated vapor pressure of water at 120 degrees Celsius. And we can look that up in the table 13-3 and it's 1.99 times 10 to the 5 pascals. So, that's going to be the pressure inside this pressure cooker. Now, the forces that are on this weight that's here upwards, there is the force due to the pressure inside and it's going to be p subscript i for inside pressure inside times the area of the opening. And that's the pressure, that's the force upwards. And then the force downwards is going to be the weight plus the force due to the air pressure outside, the atmospheric air pressure. And normally when we have a Freebody diagram, we have a force arrow downwards for weight, we don't often add this pressure force because usually the underside of the object has the same air pressure which is going upwards and then it cancels out anyway. But this scenario is slightly different because the pressure below this thing is different, is the pressure inside the pressure cooker. So, we have the force up has to equal to force down and if this weight to stay there. So, Pi A equals Fg plus Pa A, that's atmospheric pressure times A. And rearrange that slightly take this term to the left hand side and you get, and then switch the sides around, you get force of gravity is the pressure inside times the area minus the pressure outside times the area. And Fg is mass times gravitational field strength, g. And that's going to be A times factored out Pi minus Pa. And the area is going to be π times the radius squared which is diameter over 2 squared times Pi minus Pa and divide both sides by g and you solve for m. So, the mass is going to be π times 3 millimeters which is times 10 to the minus 3 meters over 2 squared times the pressure inside, 1.99 times 10 to the 5 pascals, minus the pressure outside, 1.01 times 10 to the 5 pascals, divided by 9.8 newtons per kilogram which gives us this many kilograms which is about 71 grams.