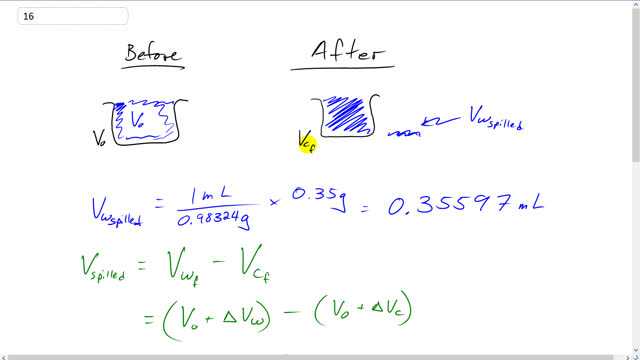
It is observed that 55.50 mL of water at $20 ^\circ \textrm{C}$ completely fills a container to the brim. When the container and the water are heated to $60 ^\circ \textrm{C}$, 0.35 g of water is lost.

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. Initially this water completely fills up the container. And so the initial volume of the water and the initial volume of the container are both the same and there's no need for a c subscript for container and a w subscript for water, the initial case they're both v naught. Now, after this is heated up, though, the container will have some final volume and the water will have some final total volume. And it turns out that the water will have a total volume that exceeds that of the container, and so some of the water spills out. So, we can figure out how much spilled out by taking the density of water and turning it, and taking the reciprocal of it and going 1 milliliter for every 0.98324 grams and times it by the 0.35 grams of water found outside the container, and that gives 0.35597 milliliters of water. And this volume spilled is the amount by which the final volume of the water exceeds the final volume of the container. So, taking them to take the difference here. Volume in the water final minus volume of the container final. So, the final total volume of the water is going to be the water's initial volume plus the change in volume of the water, and we're gonna go minus the final volume of the container which is the container's initial volume plus its change in volume and v naught being the same for both, but, and then they make 0, you know, v naught minus v naught. And we're left with the volume of water spilled is the change in volume of the water minus the change of volume in the container. And then using our formula for change of volume, it's going to be the coefficient of linear expansion of water times v naught times Δt minus coefficient of linear expansion for, or, sorry, volume expansion for the container times v naught Δt. And we can solve for βc. We'll take the left side which makes it positive and bring v spill to the right hand side making it minus. So, we have βc v naught Δt equals βw v naught Δt minus v spilled and divide both sides by v naught Δt and you solve for the coefficient of volume expansion for the container. So, that'll be coefficient of volume expansion for water times the initial volume times change of temperature minus the volume of water spilled divided by the initial volume times temperature change. So, it's 210 times 10 to the minus 6 coefficient of volume expansion for water times 55.5 milliliters initial volume times a change a temperature of 62 degrees final temperature minus 20 degrees Celsius initial temperature minus 0.35597 milliliters of volume of water spilled that we calculated before. And divide that by 55.5 times 40 Celsius degrees and this gives about 50 times 10 to the minus 6 for the coefficient of volume expansion for the container. And when we look at the table of coefficients we see that the one that's closest to this is copper, the container must be made of copper.