Estimate the time needed for a glycine molecule (see Table 13–4) to diffuse a distance of in water at if its concentration varies over that distance from to ? Compare this “speed” to its rms (thermal) speed. The molecular mass of glycine is about 75 u.
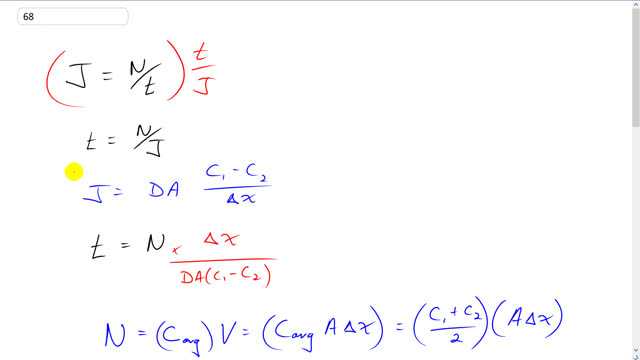
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. J is the diffusion rate, it's the number of molecules that past a certain point per time. And we can solve this for t by multiplying both sides by t over J. And the left side becomes t and on the right hand side we have J in the bottom. So, t is the number of molecules divided by the diffusion rate, J. And we have another fancy equation for J it's the diffusion constant times the cross sectional area that's being crossed times the difference in concentrations between the two points, point 1 and point 2, divided by the distance between those points. So, when we substitute this into our equation for t, we're going to multiply by the reciprocal of J instead of dividing by it. So, we have t equals number of molecules times Δx over DA times C1 minus C2. So, the number of molecules is going to be the average concentration between the two points times the volume enclosed, you know, by the area and the distance between the two points. And so this is like a cylinder with some volume, V. And that's gonna be the area times the distance between the two points, Δx. And C average is going to be C1 plus C2 over 2. And that'll be true if there's, if the concentration gradient is even. But anyway. So, we have to make some assumption somewhere and that's a reasonable one. So we have C1 plus C2 over 2 times A times Δx. So, when we plug that in for the number of molecules we have some things that cancel, the A's cancel and the Δx becomes squared. And so now our time then is going to be the sum of the concentrations times Δx squared over 2 times the diffusion constant times the difference in concentrations. So, we have 1 mol per cubic meter initially plus 0.5 moles per cubic meter at the point 2 and then we have 25 micro meters between them and we multiply by 10 to the minus 6 to turn into meters, and square that, divided by 2 times the diffusion constant for glycine which is 95 times 10 to minus 11 meter squared per second, we have to look that up in the table there. And times by the difference in concentrations, 1 minus 0.5. And you get about 0.99 seconds. So, the speed at which is diffusing is the distance is traveling divided by the time it takes to do it, so that's 25 micrometers divided by 0.99 seconds and that gives 2.5 times 10 to the minus 5 meters per second. And the rms speed of these molecules is square root of 3 times Boltzmann's constant times the absolute temperature in kelvin divided by the mass of a single molecule. So, that's square root of 3 times 1.38 times 10 to the minus 23 joules per kelvin times 20 degrees Celsius plus 273.15 divided by 75 atomic mass units per glycine molecule times by 1.6605 times 10 to the minus 27 kilograms per atomic mass unit and that gives us kilograms in the bottom then. And then it's the mass of one glycine molecule. And that gives 312.17 meters per second is the diffusion or the rms velocity, you know, that it's moving around randomly due to its thermal energy. And taking the ratio of these two we have 2.533 times 10 to the minus 5 meters per second divided by 312 meters per second which is 8.1 times 10 to the minus 8. So, there's a both 7 orders of difference or orders of magnitude difference between the diffusion speed versus the rms speed which we expect because this diffusion speed is, is the speed at which it goes from one point linearly to another. Whereas or, you know, diffusion speed is like that. Whereas the rms speed is going in all kinds of directions. And, so, I mean, ultimately the results in this diffusion and... But the speed is going to be much greater. Hope that make sense.
