GiancoliAnswers

You are here

  4. Problem 10
Select a problem
Question: 

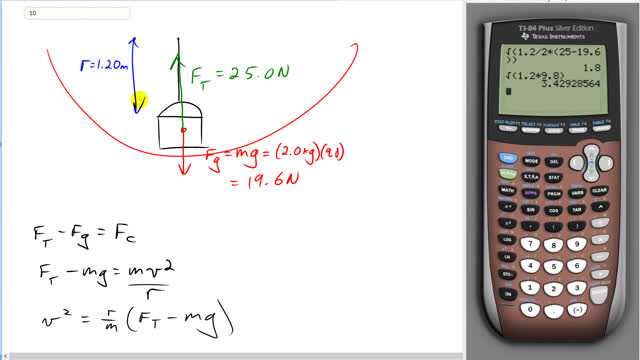
A bucket of mass 2.00 kg is whirled in a vertical circle of radius 1.20 m. At the lowest point of its motion the tension in the rope supporting the bucket is 25.0 N.

  1. Find the speed of the bucket.
  2. How fast must the bucket move at the top of the circle so that the rope does not go slack?

Source: Giancoli, Douglas C., Physics: Principles with Applications, 7th Edition, 2014.

Quick Answer: 
  1. $1.80\textrm{ m/s}$
  2. $3.43\textrm{ m/s}$

Giancoli 7th Edition, Chapter 5, Problem 10

(2:16)

Chapter 5, Problem 10 is solved.

View sample solution

Transcript for this Giancoli solution

This is Giancoli Answers with Mr. Dychko. This bucket is whirled in a vertical circle of radius 1.2 meters at the bottom of the circle. The tension of the string that makes it keep on going in a circle and brings it back up is 25.0 newtons. And there's a weight down on the bucket equal to mg of 2 kilograms times 9.8 newtons per kilogram, which is 19.6 newtons. So the free-body diagram leads us to this equation for the net force; the tension force upwards minus gravity downwards is the net force and the net force is the centripetal force and that's equal to ma, where a is v squared over r— centripetal acceleration. So we have F T minus mg equals m v squared over r because m v squared over r is the centripetal force. And, we'll multiply both sides by r over m. And we get v squared is r over m times tension force minus weight. So, v is the square root then of r over m times F T minus mg. So that's 1.20 meters over 2 kilograms times 25 newtons minus 19.6 newtons which is 1.80 meters per second must be the speed at the bottom of the circle. And, if the bucket is going such that at the very top of the circle, there is no tension and the centripetal force is entirely provided by gravity then the speed which is that point between when the rope is almost slack but not quite is when the centripetal force is equal to gravity. And that makes m v squared over r equal to mg substituting for centripetal force and substituting for gravity. And we can solve for v by multiplying both sides by r, divide both sides by m and take the square root of both sides. So, v is square root 1.20 meters times 9.8, which is 3.43 meters per second.