
A car drives straight down toward the bottom of a valley and up the other side on a road whose bottom has a radius of curvature of 115 m. At the very bottom, the normal force on the driver is twice his weight. At what speed was the car traveling?
In order to watch this solution you need to have a subscription.
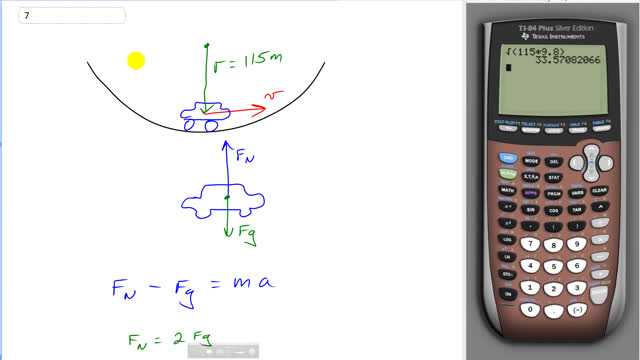
This is Giancoli Answers with Mr. Dychko. Here's a picture of what's happening with this car traveling down through this valley. At the bottom of the curve, it's going through a circle of radius 115 meters and has some tangental velocity, or some speed, this way. The free-body diagram looks like this, with the normal force upwards, with an arrow that's twice as long as the gravity downwards because we are told the normal force is 2 times gravity. And so we can draw, write Newton's second law, with these forces; we have the up forces minus the down forces equals mass times acceleration. And so, normal force minus gravity equals ma. And then make substitutions for each of these things; we can say normal force is 2 times gravity coz we are told that by the question; gravity is mass times gravitational field strength, g, and then acceleration since it's accelerating in a circle going at constant speed, the acceleration is centripetal acceleration so we can write v squared over r instead of a. So we now make substitutions into Newton's second law from here. So we have normal force then is 2 times force of gravity so that's 2 times mg, and force of gravity is mg. And then we have mass copied and then times acceleration, v squared over r. The m's cancel everywhere; and divide both sides by m and 2 g minus g makes g and we have g is v squared over r. And then we solve for v by multiplying both sides by r and take the square root of both sides and we have the speed must be the square root of the radius of curvature times g. So square root of 115 meters times 9.8 meters per second squared which is 33.6 meters per second.