
A proposed space station consists of a circular tube that will rotate about its center (like a tubular bicycle tire), Fig. 5–39. The circle formed by the tube has a diameter of 1.1 km. What must be the rotation speed (revolutions per day) if an effect nearly equal to gravity at the surface of the Earth (say, 0.90 g) is to be felt?
In order to watch this solution you need to have a subscription.
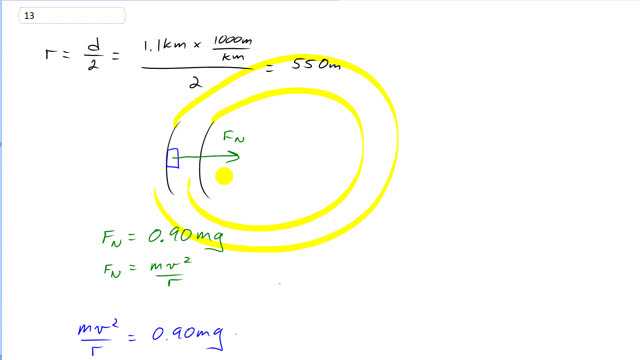
This is Giancoli Answers with Mr. Dychko. So the rotation of this spaceship, this tubular circular spaceship causes an apparent weight, you know, it would feel the same as weight on Earth would; weight on Earth just feels like a normal force of the ground pushing up on you and in the same way, if you were standing in this spaceship, you would feel a normal force due to the outer wall of the spaceship, as it pushes you in a circle. And so what speed of rotation does this spaceship have to have in order to make that normal force about 0.9 times the weight you would experience on Earth, mg? So 0.9 times the mg is the normal force. The normal force also is the centripetal force and it's mass times centripetal acceleration and that's gonna make it mass times v squared over r because centripetal acceleration is v squared over r. So we can equate these two things to each other; mv squared over r is 0.9mg. And r, by the way, is 1.1 kilometers times a 1000 meters per kilometer to turn it into meters, divide by 2. So, we have 550 meters for the radius. And then we go square root 0.9 times 550 meters times 9.8 meters per second squared and, not sure if I mentioned the algebra here, but the m's canceled times both sides by r and then take the square root of both sides to solve for v and you end up with 69.6491 meters per second; now that's for the revolutions per day. So, we'll take this speed of a point on the edge of the spaceship so that v here is 69 point whatever. And we'll times it by 1 revolution for every 2π times radius meters; this is a circumference, 2πr formula here. And so you have one revolution as you travel through the distance of one circumference and that's gonna cancel away the meters and times by 3600 seconds per hour times 24 hours per day and you end up with revolutions per day. And that's 1700 revolutions per day when you round it to two significant figures.