
A horizontal force of 310 N is exerted on a 2.0-kg ball as it rotates (at arm’s length) uniformly in a horizontal circle of radius 0.90 m. Calculate the speed of the ball.
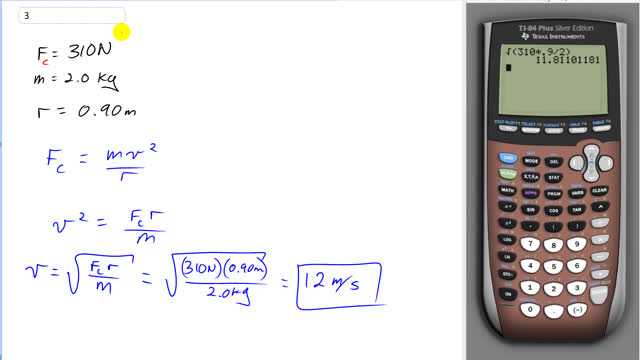
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. The centripetal force on the ball is 310 Newtons and it has a mass of 2 Kilograms and it travels in a circle of radius 0.9 meters. And we always start a question by just writing down all the stuff that we know. And the formula connects all these things with the speed of the ball, which we have to find, is the centripetal force is m v squared over r. And we multiply both sides by r and divide by m and that cancels the m and the r on this side and introduces it over there. And switch the sides around, and we get, speed squared equals centripetal force times r divided by m and take the square root of both sides to solve for the speed. So speed is square root of centripetal force times the radius of curvature divided by mass. So that's 310 Newtons times 0.9 meters divided by 2 Kilograms all square rooted and with two significant figures, this rounds to 12 meters per second.