
Neptune is an average distance of from the Sun. Estimate the length of the Neptunian year using the fact that the Earth is from the Sun on average.
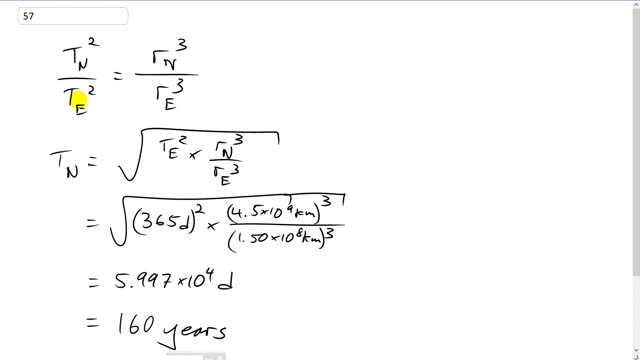
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. Kepler's third law says that when you take the square of the period of one planet around the Sun, and divide it by the square of the period of some other planet orbiting the Sun, that's gonna equal the cube of the first planet's average distance from the Sun divided by the cube of the other planet's average distance from the Sun. So we can solve this for the period of Neptune by multiplying both sides by the period of Earth, which we know to be 1 year. Multiply both sides by period of Earth squared and then take the square root of both sides and you get this; and you could even, you know, if we wanted to simplify it a bit more, we could write T Earth, take it out from under the square root sign, if you like it, and then have r Neptune cube divided by distance from the Earth to the Sun, cubed. Anyway, we get a square root of 365 days squared times 4.5 times 10 to the 9 kilometers; and now normally, I would turn this kilometers into meters because we typically like—meters, kilograms and seconds—in our formulas, and that would be fine if you did. But I didn't bother because it's kilograms, or kilometers cube divided by kilometers cube and I know that these units are just going to cancel anyway and they won't matter; so long as they are the same, they are gonna cancel and we are gonna be left with the square root of days squared, which is days. So here's the Neptune distance from the Sun average and here's the average distance from the Earth to the Sun, cube both of those distances, divide them, multiply by the 1 Earth-year in days, 365 days squared, square root that whole result and you get about 160 years is the period of Neptune's revolution around the Sun.
you should have left it as 164 years