
A jet pilot takes his aircraft in a vertical loop (Fig. 5–38).
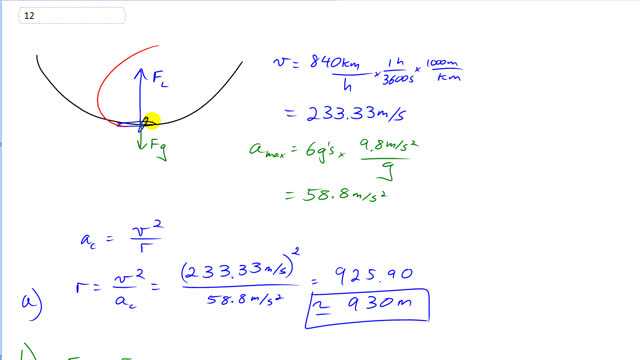
- If the jet is moving at a speed of 840 km/h at the lowest point of the loop, determine the minimum radius of the circle so that the centripetal acceleration at the lowest point does not exceed 6.0 g’s.
- Calculate the 78-kg pilot’s effective weight (the force with which the seat pushes up on him) at the bottom of the circle, and
- at the top of the circle (assume the same speed).

In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. At the bottom of this pilot's looped trajectory, we have the lift force going upwards and gravity going down then lift force is much greater than gravity because it has to lift the plane back up into this circle as it goes back up along this curved path here. Well, let's take care of some bookkeeping first as we often do. So, we have the speed that this plane is going is 840 kilometers an hour but we'll convert that into meters per second by multiplying by a 1000 and dividing by 3600 and we see that the meters or kilometers cancel and the hours cancel and we are left with meters per second. That's the same as dividing by 3.6 so we get 233.33 meters per second is the speed of the jet. The maximum centripetal acceleration it can have at the bottom of this loop is 6g's and we'll convert that into meters per second squared. So, we have 9.8 meters per second squared per g; the g's cancel giving us 58.8 meters per second squared. We know that centripetal acceleration is v squared over r and we'll solve this for r to find out what radius of curvature this path should have so that the acceleration is 6g's. So, we'll times by r over a c and the a c cancels on the left and the r cancels on the right leaving us with r equals v squared over centripetal acceleration. So that's 233.33 meters per second squared divided by 58.8 meters per second squared gives us about 930 meters is the radius of this loop. And then for part B, we use that free-body diagram to talk about the lift force upwards minus gravity downwards has to equal ma, that's gonna be the net force and a is centripetal acceleration which we have already calculated is 58.8 meters per second squared. So, the lift force is the apparent weight of the pilot; it's the normal force that they experience being pushed up by the seat and we'll add F g both sides here to solve for the lift force. And lift force is m times acceleration plus gravity so that's ma c plus mg and you can factor out the m's and you get 78 kilograms times 58.8 meters per second squared plus 9.8 meters per second squared and let's figure out what that makes. 78 times 58.8 plus 9.8 makes about 5400 with two significant figures. That's the apparent weight at the bottom of the loop. At the top of the loop, the pilot will will have gravity downwards and then it's kind of a misnomer, it's kind of confusing to call this a lift force because it's actually gonna be a force that's pushing down towards the ground to keep the plane going downwards in this loop. So, it goes down along this path but I'll just keep calling it a lift force; it's the force you know that the wings are, you know, the air is pushing on the wings and then the wings push the plane down with this force. OK So they are both pointing in the same direction in the direction of acceleration and so we will call the radial direction towards the center positive. So that makes gravity positive and the lift force positive equals mass times acceleration; acceleration is v squared over r because we can see the acceleration is in a circle… it's radial so it's v squared over r and substituting for gravity is mg. And then we solve for this lift force and we'll subtract mg from both sides here and we get lift force is mv squared over r minus mg; factor out the m and you get m times v squared over r. 78 kilograms times 233.33 squared over 925.9 and then minus 9.8 and we get about 3800 newtons is the effective weight at the top of the loop.
For part c, how can you be certain to use 233.33 m/s as your velocity if this is the velocity give by the problem for the lowest point of the loop? I solved the problem by using 6.0g as my radial acceleration (i got the correct answer but I'm not sure why). Thank You.
Oops I misread the part where it said "same speed".