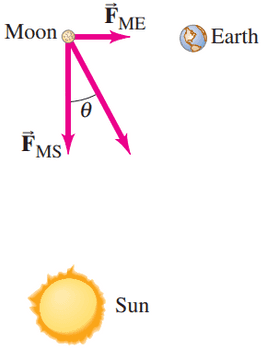
Find the net force on the Moon $(m_M = 7.35 \times 10^{22} \textrm{ kg})$ due to the gravitational attraction of both the Earth $(m_E = 5.98 \times 10^{24} \textrm{ kg})$ and the Sun $(m_S = 1.99 \times 10^{30} \textrm{ kg})$, assuming they are at right angles to each other, Fig. 5–43.

VIDEO TRANSCRIPT

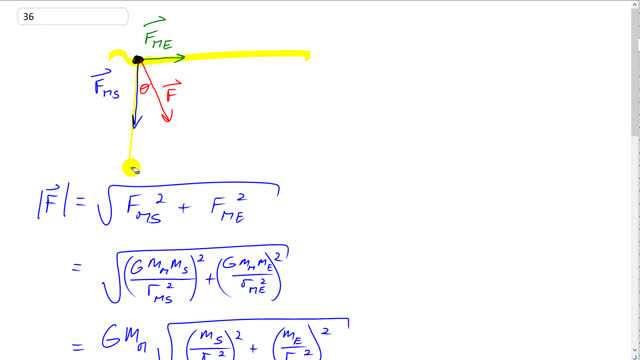
This is Giancoli Answers with Mr. Dychko. So the moon is situated here with the Earth pulling it straight to the left and the Sun pulling it straight down and these forces are at right angles we are told and our job is to calculate what the net force is including its direction, Θ. So, the magnitude of this net force is gonna be the square root of the sum of the squares of each of these forces; since they are right angles, we can use Pythagoras. You can imagine this is a triangle with this force down here, like this. So, it's a right triangle. So, we can use Pythagoras to calculate the hypotenuse. And substituting for each of these forces, we have the gravity formula G times mass of the moon times mass of the Sun divided by the distance from the moon to the Sun squared and then that whole result gets squared because we are using Pythagoras plus the same formula for the moon and the Earth and square that. The G squared, square root of it is just G; it's a common factor, we can factor it out. and we can factor out m—mass of the moon—squared and then out of the square root, it becomes just mass of the moon, exponent 1. And then we are left inside with mass of the Sun divided by distance from the moon to the Sun squared all squared and then mass of the Earth divided by distance from the moon to the Earth squared, all squared. And that ends up being this and we have 6.67 times 10 to the minus 11 newton meter squared per kilograms squared universal gravitational constant times—mass of the moon—7.35 times 10 to the 33 kilograms times the square root of— the mass of the Sun— 1.99 times 10 to the 30 kilograms divided by distance from the Sun to the moon squared and we have mass of the Earth, in kilograms, divided by the distance from the moon to the Earth squared and all gets squared and here's what it looks like on the calculator and I'm using this capital E notation for doing scientific notation, which I really recommend and on the bottom you will notice, we have like 149.6 times 10 to the 9 squared and then close bracket that closes this bracket here and then that whole fraction gets squared plus the same sort of deal with the Earth and moon distance; gets squared and then close bracket that whole term gets squared. And we end up with 4.79 times 10 to the 20 newtons is the net force. And then the direction is the inverse tangent of the Earth-moon force divided by the moon-Sun force. So that's opposite over adjacent opposite, you know, being that I'm imagining this down here again right. So, we substitute for each of these forces using the regular formula and then reduce it to this by canceling the G and the mass of the moon on top and bottom and then multiply top and bottom by this which gets rid of it from the top and puts it down here multiplied by the mass of the Sun. And then the same idea with the distance from the moon to the Sun multiplied, top and bottom, by it and on the bottom when you multiply this fraction by distance from the moon to the Sun squared is gonna disappear from the bottom and it's gonna appear on top, as shown here. And then substitute in the numbers and let's see what we get. We have inverse tangent of 5.98 times 10 to the 24 times 149.6 times 10 to the 9 squared divided by 1.99 times 10 to the 30 also divided by 384 times 10 to the 6 and what do we have there. That looks like it's about 24.5 degrees; that's what Θ is in that diagram and there we have it!