
Table 5–3 gives the mean distance, period, and mass for the four largest moons of Jupiter (those discovered by Galileo in 1609). Determine the mass of Jupiter:
- using the data for Io;
- using data for each of the other three moons.
- yes, the results are consistent.
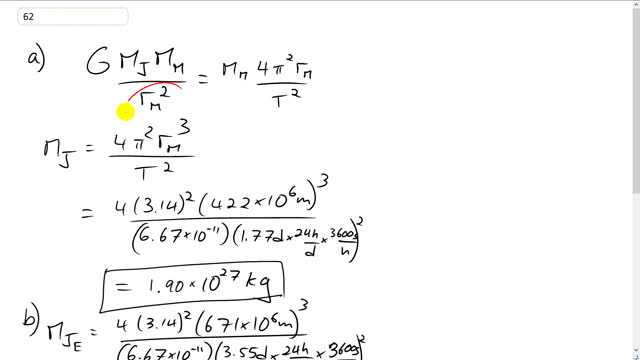
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. The force of gravity on a moon orbiting Jupiter is gonna be g times mass of the Jupiter times mass of the moon divided by the distance to the moon from the center of Jupiter squared. And that force of gravity is the centripetal force so it equals mass of the moon times its acceleration. And I have written acceleration as 4π squared times the orbital radius divided by period squared because normally, it's v squared over r but we can think of v as being the circumference of its orbit divided by the period of an orbit; that's distance over time here. That's the size of the circle divided by the time it takes to do one circle. That's v and then we square that and divide by r and this turns into 4 π squared r over T squared, and that's what I have written here. And we can solve for this mass of Jupiter by dividing both sides by mass of the moon; turns out to be not relevant, it cancels. And then multiply both sides by distance to the moon squared, divide by G and you end up with distance to the moon cubed times 4 π squared divided by period squared and there's also a G down there too. There. So, we have 4 times π squared times 422 times 10 to the 6 meters as the average orbital radius of the moon Io, cube that, divided by 6.67 times 10 to the minus 11 and then times by the orbital period squared and they have to convert that into seconds because you always want meters, kilograms and seconds units in your formula unless you can see that some units are gonna cancel and they don't matter. But, when in doubt, always convert into mks units. So, at 1.77 days times 24 hours per day times 3600 seconds per hour; here's the number of seconds, square that, and you get 1.90 times 10 to the 27 kilograms must be the mass of Jupiter. And then we can use the data from the other moons. We have Europa, Ganymede and Callisto. So, when we use the data from all these other moons, it should be C for Callisto, we get the same result pretty much. We get 1.90 times 10 to the 27; they differ in the higher precision digits but, you know, within the error of our data; within, we have about three significant figures I guess; we see only a small difference here when we use Ganymede. But otherwise, it's pretty consistent that the mass of Jupiter is estimated to be 1.90 times 10 to the 27 kilograms.