At what distance from the Earth will a spacecraft traveling directly from the Earth to the Moon experience zero net force because the Earth and Moon pull in opposite directions with equal force?

VIDEO TRANSCRIPT

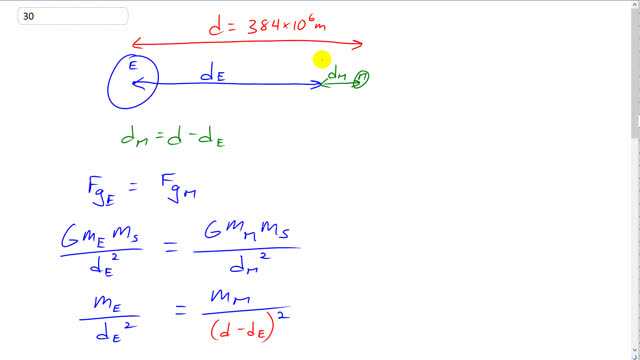
This is Giancoli Answers with Mr. Dychko. The distance from the center of the Earth to the spacecraft, we'll label it d subscript E and then we have the distance to the moon and we know that this position, where there is zero net force of gravity on the spacecraft, has to be closer to the moon than it is to the Earth because the moon is so much less massive; we have to get closer to it for its force to get up to the point where it can match the force exerted by this mass of Earth. Now, to reduce the number of variables, we can use this value for the distance between the Earth and moon center's, 384 times 10 to the 6 meters to express this d subscript M, in terms of d E. So the distance to the moon is the total distance, which we know, minus d E. And then when we read our gravity due to the Earth equals gravity due to the moon formula, we can substitute for d M and write d minus d E in its place. And then we have an equation with only one unknown, which we can solve. So this is gravitational constant times mass of the Earth times mass of the spacecraft divided by distance to the spacecraft from the Earth squared equals the force of gravity exerted by the moon, G mass of the moon times mass of the spacecraft divided by the distance to the moon squared. And the G's cancel and so does the mass of the spacecraft and so this position is does not depend on the spacecraft's mass, as it turns out. And, we have also made a substitution here for that distance to the moon in terms of the distance from the Earth. So, we'll take the reciprocal of both sides by raising both sides to the exponent negative 1 to get our unknown in the numerator which is a easier place to work on it, with unknowns in the numerator. And then we'll take the square root of both sides to get rid of that square there. And so we have d E over square root of mass of the Earth equals d minus d E divided by square root mass of the moon. And then, we get rid of the denominators here by multiplying by square root mass of the moon and also multiplying by square root mass of the Earth both sides and mass of the Earth cancels there leaving us with distance to the Earth times square root mass of the moon equals d times mass of the Earth minus d to the Earth times square root mass of the Earth. And we'll put both the d E terms on the same side and when we move this to the left, it becomes positive and so we can factor out this common factor, distance to the Earth multiplied by square root mass of the moon plus square root mass of the Earth equals total separation between the Earth and the moon times square root mass of the Earth and then divide both sides by this bracket here to get that the distance to the Earth from this position where there's zero force of gravity is separation between the Earth and the moon times square root mass of the Earth divided by the sum of the square roots of the masses of the Earth and the moon. And on the calculator, it looks like this. So, we have 384 times 10 to the 6 meters times square root 5.98 times 10 to the 24 kilograms—mass of the Earth— divided by square root of 7.35 times 10 to the 22 kilograms—mass of the moon— plus square root mass of the Earth and we get 3.46 times 10 to the 8 meters is the distance from the Earth, Earth's center I should say, to the point where there is zero net force due to gravity.