Estimate the acceleration due to gravity at the surface of Europa (one of the moons of Jupiter) given that its mass is $4.9 \times 10^{22} \textrm{ kg}$ and making the assumption that its mass per unit volume is the same as Earth’s.

VIDEO TRANSCRIPT

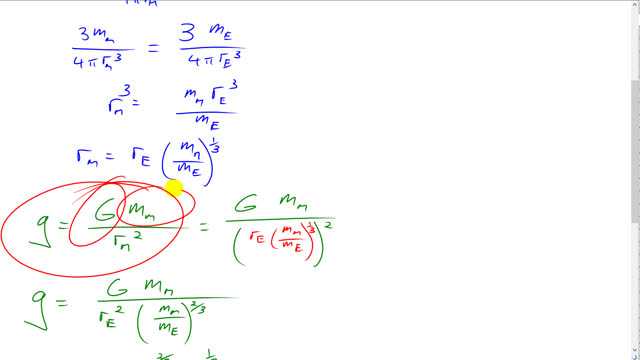
This is Giancoli Answers with Mr. Dychko. We know the acceleration due to gravity formula is this one where acceleration due to gravity on Europa would be universal gravitational constant, G times the mass of this moon divided by its radius squared. But we don't know what its radius is and so we have to do a bit of work to use the information we do know -- that it has the same density as Earth; that's another of way of saying it has the same mass per unit volume as Earth and in order to figure out what the radius of Europa is. So the density of Earth is the Earth's mass divided by its volume and that's the mass of Earth divided by four-thirds πr cubed -- that's the volume formula, where r is the radius of the Earth. and that's the same as writing 3 times mass of the Earth over 4 πr E cubed; when you multiply top and bottom by 3, and this 3 will cancel there leaving us with a 3 on top. Just a neater way of writing this; it's nice to not have fractions within fractions. So, we're told that the mass of the moon Europa equals the mass of the Earth or sorry, density there -- that those are densities same -- same mass per unit volume, in other words. And the density of the moon is well, the same formula as the density for the Earth but just substituting in the moon's mass and radius. So these two things are equal to each other - this density for the moon equals this density for the Earth. And then we do some algebra to solve for the radius of the moon. So, what I did is I canceled the 3, 4 and the π because they are common factors on both sides and raise both sides to the exponent negative 1, or also known as taking the reciprocal of both sides so that we get this unknown in the numerator and so it's r moon cubed over mass of the moon. Maybe I could show that I guess. r moon cubed over mass moon equals radius Earth cubed over mass Earth -- that's what happens after you do this exponent negative 1 to both sides -- and then multiply both sides by mass of the moon and you end up with this. So then you take the cube root of both sides, and taking cube root is the same as using exponent one-third. That's a math thing that you need to know that -- let's get the exponent back where it belongs -- that the index of a radical, that's what the name of this, you know, square root sign is but it's not always a square root, it always depends on what number is here and if there's no number then you just assume it's a 2 for square root but sometimes it's a 3 or a 4 and in this case, it was a 3; you can always write that index as the denomintor of an exponent and it's the exact same thing and in this way, it's easier to plug into our calculator when we write it as an exponent. So, it's exponent one-third for cube root. So, the radius of the moon Europa equals the radius of the Earth times the ratio of masses to the exponent one-third. So, here's the regular acceleration due to gravity formula for the moon; I guess, I could put a subscript capital M on that g there. And, we'll substitute for the radius of the moon from here and that's what we have done in red here. Now, this radius is squared and so we end up with radius of the Earth squared and then mass of the moon divided by mass of the Earth to the power of one-third squared is ends up being to the power of two-thirds. And then, we end up with mass of the moon to the power of 1 divided by mass of the moon to the power of two-thirds makes mass of the moon to the power of one-third. When dividing powers, you subtract the exponents so 1 divided by two-thirds is one-third. And when you, you know, this mass of the Earth to the power of two-thirds can go in the numerator by multiplying top and bottom by mass of the Earth two-thirds and then it cancels here and then it ends up here as shown here. And then substitute in the numbers and we are done. So that's 6.67 times 10 to the minus 11 newton meter squared per kilogram squared and notice in the calculator, the way I am doing the exponents and I think it's nice to see this technique because it avoids some calculator button-pushing errors. So, I'm using a second function capital E to say, times 10 to the power of and it's useful to do it that way because the calculator understands that this 5.98E24 is a single value; it's a single value so when you go exponent two-thirds, that exponent is being applied to this whole thing, not just to the 24 -- that would be silly to apply this exponent just to the times to the 24 -- you want to apply the exponent to the whole thing and the calculator understands that when you use this notation as opposed to 5.98 -- sometimes I see students doing this -- times 10 to the power of 24 and things can get complicated because if you do this and then go exponent two-thirds, this is totally not right. The only thing that will get raised to the power of two-thirds is this 10 to the power 24 and it's gonna ignore the 5.98 because that's some other number over here to the left of the multiply sign. So, bad stuff there, get rid of that. Use this capital E notation instead and life would be easier and you would need fewer brackets. I mean, you could get away if you are with the times this notation, if you go, well, I see I even forgot it and what I'm trying to demonstrate, you put a bracket over here and you can get away with that. But boy, now you have lots of brackets and you might forget some. So, use this capital E and you don't have to worry about the brackets. So this would be correct here but I just recommend against it. There, get rid of it. So, there we have it -- times by the mass of the Earth raised to the power two-thirds times the mass of this moon raised to the power of one-third divided by radius of the Earth squared and you get 2.0 meters per second squared with two significant figures as the acceleration due to gravity on Europa.