
Tarzan plans to cross a gorge by swinging in an arc from a hanging vine (Fig. 5–42). If his arms are capable of exerting a force of 1150 N on the vine, what is the maximum speed he can tolerate at the lowest point of his swing? His mass is 78 kg and the vine is 4.7 m long.

In order to watch this solution you need to have a subscription.
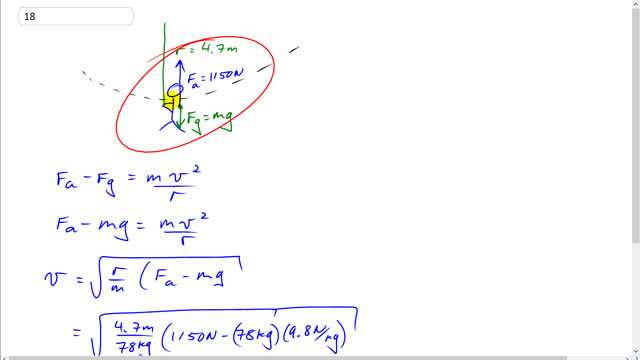
This is Giancoli Answers with Mr. Dychko. When Tarzan is swinging on this, 4.7 meter long vine at the bottom of the arc, they will have this picture for the forces, the free-body diagram will have the applied force of his arms upwards and gravity pulling down and the up force minus the down force is gonna equal mass times acceleration and acceleration, in this case, is v squared over r because it's centripetal acceleration and we'll substitute m g in place of F g, for gravity, and then we'll solve for v; we'll multiply both sides by r over m, and the r and m cancel there, and we are left with v squared all this but then we'll take the square root of both sides to solve for v. So v is the square root of r over m times the arm force minus weight. So we have a square root of 4.7 divided by 78 kilograms times 1150 newtons minus 78 kilograms times 9.8 newtons per kilogram, that gives 4.8 meters per second is the maximum speed Tarzan could have at the bottom of a swing.