How large must the coefficient of static friction be between the tires and the road if a car is to round a level curve of radius 125 m at a speed of 95 km/h?

VIDEO TRANSCRIPT

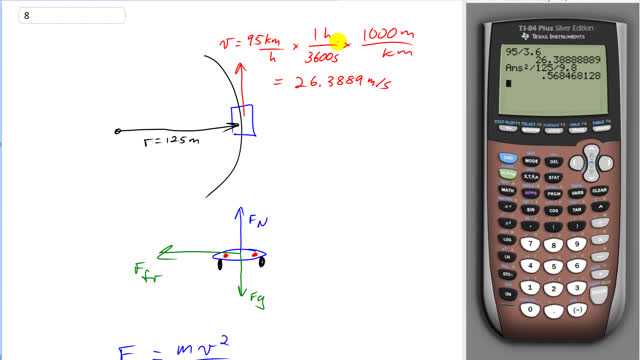
This is Giancoli Answers with Mr. Dychko. This car is traveling in a radius of 125 meters and we will convert this 95 kilometers per hour, speed into meters per second by multiplying by 1 hour for every 3600 seconds and the hours cancel and then times by 1000 meters per kilometer and the kilometers cancel leaving us with meters per second; this is the same as dividing by 3.6. So I convert that into 26.3889 meters per second. Now, we wanna have a free-body diagram of the car in order to understand the forces on it and this is a tail lights view, view from the back of this car; So, this is a top-down, like satellite view and this would be a view from, you know, from driving behind the car, these red dots are supposed to be the tail lights and here's the black tyres and so on. So, we have the friction force acting to the left, accelerating it in this circle; that's the centripetal force. And there's a normal force going upwards applied by the road on the car and gravity downwards. And this normal force up is gonna equal gravity down because there's no vertical acceleration of the car; it's not lifting off the road or going into the road. OK. So, centripetal force is mv squared over r. It's because you know, acceleration is v squared over r and centripetal force is the net force here and it equals mass times acceleration but this is the usual expression for the case where you have acceleration in a circle, with constant speed. And centripetal force, we have already mentioned, is the friction force here. Friction is what's providing that centripetal force and friction is coefficient of static friction times the normal force and the normal force is equal to gravity down which is mg. So, we'll rewrite this equation by substituting for centripetal force, and writing µ s mg instead. And then copy the m v squared over r here. And the m's cancel from both sides, which is kind of interesting; it means that this coefficient that's required, does not depend on the mass of the car and we divide both sides by g or times by 1 over g. And you end up with coefficient of static friction needed is v squared over r g. So, that's 26.3889 meters per second squared divided by 125 meters times 9.8 meters per second squared which gives 0.57.