
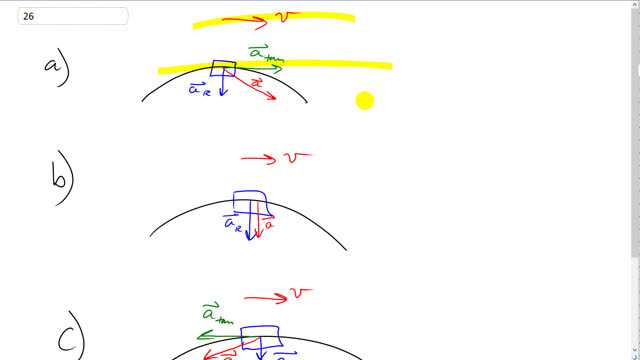
For each of the cases described below, sketch and label the total acceleration vector, the radial acceleration vector, and the tangential acceleration vector.
- A car is accelerating from 55 km/h to 70 km/h as it rounds a curve of constant radius.
- A car is going a constant 65 km/h as it rounds a curve of constant radius.
- A car slows down while rounding a curve of constant radius.
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. With this car traveling to the right along the circle and when it's speeding up, that means that the tangental acceleration will be in the same direction as the velocity, so that will be to the right. It has centripetal acceleration, or radial acceleration, pointing towards the center of the circle that it's traveling in. And the resultant acceleration is the vector sum of the tangental and the radial accelerations. So, use the parallelogram method to get that. You can imagine, a parallelogram made with the tangental acceleration and radial acceleration gives you, this one in red, the total acceleration. In part (b), it's going at constant speed so there's no tangental acceleration; there's only radial acceleration and so the resultant acceleration is just the same. And that's all there is to that one. And then in part (c), it's slowing down so the direction is to the right; but the acceleration is gonna be opposing the velocity and centripetal acceleration is still towards the center of the circle and this red arrow is the vector sum of the tangental and the radial accelerations; that should be a subscript R for radial there. You can imagine a parallelogram like this.