
Giancoli's Physics: Principles with Applications, 7th Edition
5
Circular Motion; Gravitation
Change chapter5-1 to 5-3: Uniform Circular Motion
5-4: Nonuniform Circular Motion
5-5 and 5-6: Law of Universal Gravitation
5-7: Satellites and Weightlessness
5-8: Kepler's Laws
Question by Giancoli, Douglas C., Physics: Principles with Applications, 7th Ed., ©2014, Reprinted by permission of Pearson Education Inc., New York.
Problem 5
Q
A 0.55-kg ball, attached to the end of a horizontal cord, is revolved in a circle of radius 1.3 m on a frictionless horizontal surface. If the cord will break when the tension in it exceeds 75 N, what is the maximum speed the ball can have?
A
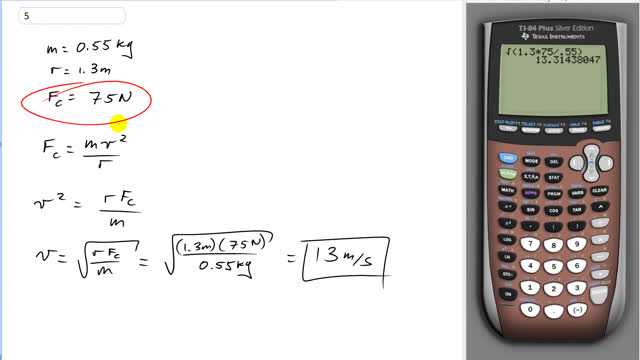
In order to watch this solution you need to have a subscription.
VIDEO TRANSCRIPT
This is Giancoli Answers with Mr. Dychko. We write down all the information we are given that the ball is 0.55 kilograms; it goes in a radius of 1.3 meters and the maximum centripetal force you can have is 75 newtons. Here's the centripetal force formula— m v squared over r and we'll multiply both sides by r and divide by m and then switch the sides around and solve for v squared; then take the square root of both sides to get v. So v is the square root of radius of curvature times centripetal force divided by mass. So square root of 1.3 times 75 newtons divided by 0.55 kilograms, which is, 13 meters per second, is the maximum speed it could have before the cord breaks.
Giancoli Answers, including solutions and videos, is copyright © 2009-2025 Shaun Dychko, Vancouver, BC, Canada. Giancoli Answers is not affiliated with the textbook publisher. Book covers, titles, and author names appear for reference purposes only and are the property of their respective owners. Giancoli Answers is your best source for the 7th and 6th edition Giancoli physics solutions.