
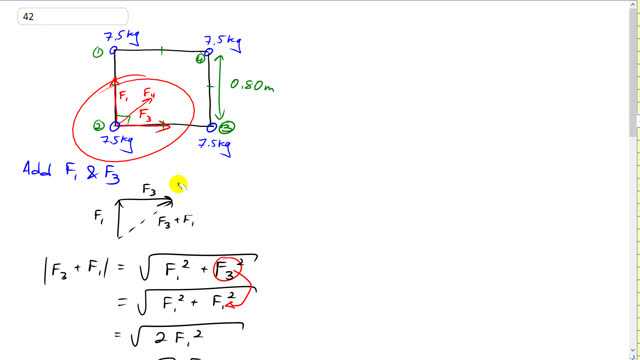
Four 7.5-kg spheres are located at the corners of a square of side 0.80 m. Calculate the magnitude and direction of the gravitational force exerted on one sphere by the other three.
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. We have a square with a side length of 0.8 meters and a mass of 7.5 kilograms at each corner and we'll find the net force on one of the masses due to the other three. There's gonna be a force upwards; let's call it force one force due to mass one and we have numbered all the masses - 1, 2, 3 and 4. Force due to mass 1 and the force due to mass 3 will be the same size forces because their masses are equal distances away; they are just different directions. And we can combine force 1 and 3 using Pythagoras because they are at right angles; it's a square after all, and we get our result there of F 3 plus 1. And then the direction of that result of force one and three will be the same as the direction of force 4 and so we can add those without any trigonometry because they are collinear; this resultant of F 1 and 3 is along the same line as force 4 because this is square and force 4 is gonna be on the diagonal, at a 45 degree angle, to a side and same with the resultant of F 1 and F 3. So we are using some shortcuts here because of the symmetry of this situation and if this mass was a different size mass than this one then the resultant of F 1 and 3 would not be along the diagonal and then we would have to use trigonometry and get into more complicated work. The concept will be the same but it would be a lot of busy work involved in calculating components and so on. So let's first do F 1 plus F 3 and that's gonna be combining F 1 and 3 using Pythagoras. And so we have a square root of F 1 squared plus F 3 squared and then down here I wrote, F 1 in place of F 3 because they have the same size and so it's 2 times F 1 squared, in other words and that's square root 2 times F 1. And then the resultant final force on this mass number 2 is going to be the result from here - square root 2 times F 1 plus the force 4. And this size force is gonna be different than the size of F 1 and 3. because the distance along the diagonal is not equal to the side length, it's gonna be further away so it's gonna be a smaller force and it's gonna be G times the one mass times other mass but they are the same size so we'll just use m squared divided by the distance to mass 4 squared. And then plus root 2 times F 1; G mass squared times distance to mass one squared. And you can factor out the G and the m squared and you have 1 over r 4 squared plus root 2 over r 1 squared. r 4 squared is r 1 squared plus r 1 squared because it's a right triangle so the distance along the diagonal here is this is r 4, that distance squared, this being the hypotenuse here is gonna be r 1 squared plus r 1 squared which is 2r 1 squared and so that's what I have written here. And substituting that in for r 4 we get this and then it makes it look a little cleaner by having a common denominator. So I multiply this term by 2 over 2 and now with the common denominator, we can add the numerator. So we have 1 plus 2 root 2 over 2 times r 1 squared and then I'll plug it into the calculator and get the answer. So we have gravitational constant times 7.5 kilograms squared times 1 plus 2 times square root 2 all divided by 2 divided by 0.8 meters squared and we get 1.1 times 10 to the negative 8 newtons is the resultant force and that's on a 45 degree angle to a side.