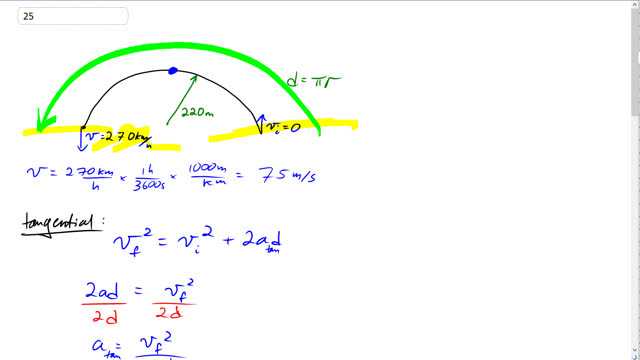
A car at the Indianapolis 500 accelerates uniformly from the pit area, going from rest to 270 km/h in a semicircular arc with a radius of 220 m. Determine the tangential and radial acceleration of the car when it is halfway through the arc, assuming constant tangential acceleration. If the curve were flat, what coefficient of static friction would be necessary between the tires and the road to provide this acceleration with no slipping or skidding?

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. This Indy500 car starts from rest here and then travels along half of a circle, a semi circle, to this point here, where it reaches the final speed of 220 kilometers an hour. And it's traveling in a semi-circle of radius, 220 meters. So we are going to figure out what coefficient of friction is needed so that it can maintain its acceleration and we are gonna consider this point here when it's halfway through the arc. But first, we are going to just figure out what tangental acceleration or what acceleration along the direction of motion, in other words, is needed to reach this final speed of 220 kilometers an hour, or 270 I should say. Let's convert this 270 into meters per second by dividing by 3.6, which is the same as multiplying by 1 hour for every 3600 seconds and the hours cancel and then times by 1000 meters per kilometer having the kilometers cancel leaving us with meters per second - 75 meters per second. And then, considering the tangental part of this question is just like a straight line -- a kinematics question -- we are just considering what the final speed will be and it squared equals initial speed squared plus 2 times the acceleration, tangental in this case, times the distance. And the distance is going to be πr. So it's half of a full circle; a full circle's circumference is 2πr and we want half of that so that's gonna make, circumference over 2 is πr. And so this d is not diameter, it's d for distance -- distance in this formula here. So, we'll get rid of this v initial squared because it's zero and we'll switch the sides around so we have acceleration on the left -- that's a tangental there -- and then divide both sides by d, or 2d, I should say, and we'll get tangental acceleration is v f squared over 2d. So, it's 75 meters per second squared divided by 2 times π times 220 meters and that is about 4.1 meters per second squared, tangental acceleration. And then for the radial direction, we need to know what the speed is at this point. The tangental acceleration is constant throughout the semi-circle but the radial or also known as the centripetal acceleration changes with speed because centripetal acceleration is the tangental velocity squared over the radius of curvature. So, as the speed increases, which it does -- it goes from 0 to 270 kilometers an hour. As the speed increases, it needs more and more centripetal acceleration. So, we have to find a specific point on this semi-circle to calculate the centripetal acceleration for and we are told to consider the point where it's halfway through the semi-circle. First, we'll find that speed then so initial speed is zero and now we have, the final speed is the square root of 2 times acceleration tangental times d. So, that's square root of 2 times a tangental times πr, which is the semi-circle, divided by 2. That's what I substituted in for d here in red it's the semi-circle divided by 2, πr over 2. And well the 2's here cancel I guess and then we have square root of aπr. So, it's square root of this tangental acceleration, 4.069 meters per second squared times 3.14 times 220 which is 53.033 meters per second. And then we need to find the radial acceleration or centripetal acceleration. So it's that speed squared divided by 220 and with two significant figures that gives us about 13 meters per second squared. And then we are told to find the coefficient of friction. So, we have friction is the resultant of the tangental force and the radial force and we can find each of these by going mass times the radial acceleration gives the radial force and mass times the tangental acceleration gives the tangental force because in each of these dimensions -- tangental and radial -- these forces are the only forces working so that makes them equal to the net force which is why you can just go mass times acceleration to find them. Gravity and normal force are acting in and out of the page here and so they are not affecting the tangental or radial directions. Although it does come into effect here because the friction force is always going to be µ times the normal force and the normal force is equal to gravity because there's no acceleration, in and out of the page, there was no acceleration vertically. So now, I wrote these vector symbols over top of this because you can't just take this number and add it to this number and divide by g because they are vectors so you have to use vector addition. And so we're gonna find the magnitude of this friction vector, by first, you know, dividing everything by this scalar m and then add the accelerations using Pythagoras. So we have square root of radial acceleration squared, which we just calculated as 12.784 meters per second squared and we'll square that plus the tangental acceleration we discovered way up there -- 4.069 meters per second squared. Square each of those accelerations, add them together, take the square root of that sum, divide by g and then get the answer. So we have square root of 12.784 squared plus 4.069 squared divided by 9.8 and that gives 1.4 is the required coefficient of friction.