
A pilot performs an evasive maneuver by diving vertically at 270 m/s. If he can withstand an acceleration of 8.0 g’s without blacking out, at what altitude must he begin to pull his plane out of the dive to avoid crashing into the sea?
In order to watch this solution you need to have a subscription.
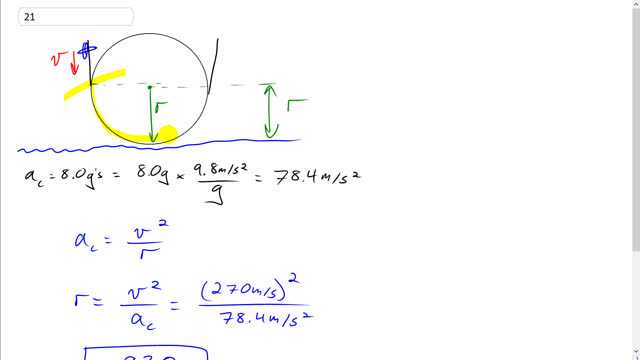
This is Giancoli Answers with Mr. Dychko. The jet pilot is traveling straight down in a dive towards the water, and they are gonna pull out of the dive at this point and they will begin traveling along this circle and then they will continue on their way there. And ignore the top part of the circle, by the way, that's just part of my drawing program, that you know, causes me to have to make a whole circle, doesn't make a half circle. So the pilot goes along their business, starts pulling out and this position, where they begin to pull out of the dive, is the same as the radius of curvature of the arc that they are gonna travel in and it also is the altitude, at which, they begin pulling out of the dive. They could pull out of the dive sooner and begin an arc up here; but then they would be traveling along a larger circle. And we want to know what the minimum altitude is at which they begin to pull out of the dive. So, what is the closest they can get to the water before they will hit the water? Given this constraint that they can tolerate only 8 g's of centripetal acceleration. So centripetal acceleration is v squared over r and we can solve this for r by multiplying both sides by r and dividing both sides by a c and we get that, the radius of curvature of this loop that they pull out in is v squared over a c, which is 270 meters per second divided by 78.4 meters per second squared— centripetal acceleration—which is about 930 meters— radius of curvature—and so that's 930 meters altitude above the sea level at which they have to begin pulling out of the dive.