If a curve with a radius of 95 m is properly banked for a car traveling 65 km/h, what must be the coefficient of static friction for a car not to skid when traveling at 95 km/h?

VIDEO TRANSCRIPT

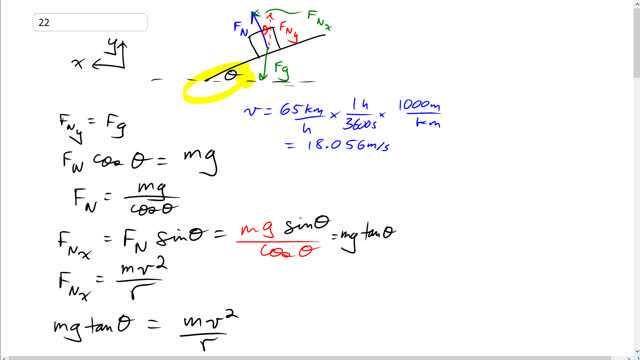
This is Giancoli Answers with Mr. Dychko. Our first step in answering this is to figure out what this banking angle must be knowing that it doesn't need any friction when the car is traveling at 65 kilometers an hour. We can draw this picture for the free-body diagram -- no friction is shown there -- and then calculate what Θ is. And then we'll use that same banking angle for the next case where there is some friction. And we'll figure out what coefficient of friction is needed in order to keep the car from slipping when it goes at 95 kilometers an hour. So, lots to do here! First, I'l say that the y-component of the normal force, in red here, has to equal gravity because there's no vertical acceleration so the total up force has to equal the total down force and there's this component of the normal force is up and so that's F N times cos Θ where this angle here is the same as the banking angle Θ and F N y is the adjacent leg of this triangle and so we use cos to calculate it. And that equals gravity which is mg. Then we can solve for F N and say that it's mg over cos Θ. And that finishes the consideration of the y-direction. And then we'll turn our attention to the x-direction. And because you know, since this is an equation with two unknowns -- we don't know the normal force and we don't know Θ -- that means we need to find some other equation to help us out. You know, if you have two unknowns, you always need two equations to solve for any of the unknowns; if you have three unknowns, you need three equations and so on. So, we wanna find Θ but we don't know F N so let's find another equation and we'll consider the x-direction to do that. So, the normal force in the x-direction, by the way, our co-ordinate system is like this where the x-axis is straight horizontal to the left, it's not along the ramp as it is for "Chapter 4" Newton's law type questions; instead, it's straight to the left and y-axis is straight up and down. And that's important because the car is accelerating straight to the left, this curve will curve to the left. We are looking at a taillights type view here but it's gonna go to the left as it goes along the curve and so that's the direction of its acceleration and so that's why we are gonna point our axis that way. And the x-component of the normal force then is F N times sin Θ is the opposite leg of this triangle. And, we can substitute for F N from what we discovered before and we'll write mg over cos Θ in place of F N and sin Θ over cos Θ is tan Θ; you have to remember that trigonometric identity. And we also know that F N x is the only force horizontally and so it's the net force making it equal to mass times acceleration and acceleration here is v squared over r since we are dealing with centripetal acceleration. And so since this equals F N x and this equals F N x, these two things equal each other as shown here. So, mgtan Θ equals mv squared over r and we can divide both sides by mg. And we get the m's canceling and we are left with tan Θ equals v squared over rg and then Θ then is the inverse tangent of the speed squared divided by the radius of curvature times the acceleration due to gravity and we get 19.298 degrees is the banking angle. So, that's the piece of data we need for our next question. Because we'll have the same curve and so the same banking angle but now the car's gonna go at 95 kilometers an hour and without friction, it would skid because 65 kilometers an hour is the fastest speed you can take this curve with no friction. But now going faster, it will need some friction and what should the coefficient of friction be, that's the question. So, there's three forces and we have our x-axis straight to the left again and our y-axis straight up and down; it's accelerating straight to the left because the curve is gonna curve to the left, just as in the picture before. And we have friction, always acting along or parallel to the surface, along the slope and so the friction is acting down the slope here. to prevent the car from riding up the slope. And it will have a component straight to the left which will contribute to the centripetal force and then we have this component of the normal force; also, directed towards the center of the curvature. And then vertically speaking, we have gravity down but we also have some component of friction, which is downwards and the vertical component of the normal force is the only upwards force that has to compensate for both of these downward forces. And so we are gonna write Newton's second law for each axis; we'll consider the y-direction first. So, we have all the up forces have to or minus all the down forces have to make zero because there's no acceleration, vertically. And so the normal force y-component minus the friction force y-component minus gravity equals zero. And we'll substitute for F N y— it's the adjacent leg of this triangle— so we'll use cos Θ times F N. And then friction force y-component, it's the opposite leg of this triangle so we'll use friction force times sin Θ. And then we'll substitute mg in place of gravity. And then we'll substitute for friction force and write it as µF N in the next line. And this is far as we can go when we consider the y-direction. Now, we have to find a new equation to help us go further because we have two unknowns; we don't know µ and we don't know the normal force. So it was two unknowns; we need two equations. So the second equation we'll get by thinking about the x-direction. And we have two forces, pointing to the left and that's the positive x-direction, as defined by our co-ordinate system. And that's the x-component of the normal force plus the x-component of friction and that's gonna be mass times acceleration, acceleration being v squared over r since it's centripetal or radial acceleration. And we can substitute for each of these F N x and force of friction, F N, x-component is the opposite leg of this triangle so we'll use sin Θ times normal force to calculate it and then friction is the x-component is the adjacent leg so we'll use cos Θ times friction. And all of that equals mv squared over r—just copied from there. And then we'll substitute for friction force as µF N and that equals mv squared over r and then we have this thing copied there. OK And that's as far as we can go with equation 2. So then we have to put on our mathematician's hat and figure out how to combine these two equations to solve for the unknown, µ. So, there's lot's of ways you can go about this. There's the addition-subtraction method where you take these two equations and add them together in such a way that you make one of the variables disappear -- that doesn't look very easy to do although it is possible. You have to use the sin squared Θ plus cos squared Θ trick in order to get rid of some of these trig terms or trig factors. But anyway. So I'm not going to do that— that's too complicated. You could solve for F N in one of the equations and then substitute it in to the other one, that will make F N disappear and then you will have an equation only containing µ and so that would be a good way to go. But the way I have chosen is to to express equation 1 in this form, where I have taken this term to the right-hand side so it's positive and then I factored out F N— that's times cos Θ minus µsin Θ— and then I took equation 2 and did the same sort of thing, where I have F N multiplied by some stuff equal some stuff. And I use the word "stuff" like that because really, the way I'm thinking is I have to have F N as a single factor times by something equals something and then the same factor multipled by something equals something. This is a nice way for things to look because we can divide these two equations and the F N's will cancel and so let's do that. We have equation 1b divided by equation 2b so I can just, you know, write a fraction there and I can see the F N's cancel and you have cos Θ minus µsin Θ over sin Θ plus µcos Θ equals mg divided by this. And dividing by a fraction is, I think it's easier to think of it as multiplying by two separate columns. So let's go mg times by the reciprocal of this— r over mv squared— and the m's cancel leaving us with rg over v squared. So there. Now, we need to isolate this µ. So we'll multiply both sides by this denominator and so it disappears from the left side. And on the right hand side, we have this rg over v squared times sin Θ. And then we also have rg over v squared times µcos Θ. And then we'll get the get rid of this denominator because fractions are messy so let's multiply everything by v squared. Notice that a lot of algebras somewhat sometimes comes down to personal preference; I tend to not like fractions and so I get rid of them and so that's why I'm doing this next line— it's not exactly something you have to do— but I am going to. So we have v squared times cos Θ minus µ times v squared sin Θ and equals rgsin Θ plus µrgcos Θ -- the v squared's cancel on the right-hand side. And then we can combine the µ terms on the same sides and bring this one to the right which makes it positive and bring this term to the left which makes it minus and then switch the sides around and factor out the µ. Then we have µ times rgcos Θ plus—because this is on the right-hand side now— plus v squared sin Θ equals v squared cos Θ— this becomes minus when it goes over there— minus rgsin Θ. And then we divide both sides by this to solve for µ. So, µ is v squared cos Θ minus rgsin Θ all divided by rgcos Θ plus v squared sin Θ. And another optional bit of trick is to make things look nice and be slick is to multiply top and bottom by 1 over cos Θ. And then you get rid of the cos Θ's here and then sin Θ divided by cos Θ is tan Θ and you get a tan Θ here and a tan Θ on the bottom as well. And so, our final formula is v squared minus rgtan Θ over rg plus v squared tan Θ and we plug in numbers and get our answer. So, let's do that. So we have open bracket to start the numerator, 26.39 squared minus 95 meters times 9.8 meters per second squared times tan of 19.298 and then close the numerator divided by denominator, 95 times 9.8 plus 26.39 squared times tan of 19.298 and optionally, close those brackets and we get 0.32—seems like we can now only have two significant figures here— and there we go. The coefficient of friction would need to be 0.32 in order for the car to not skid as it goes around the curve at 95 kilometers an hour.