
At the surface of a certain planet, the gravitational acceleration g has a magnitude of . A 24.0-kg brass ball is transported to this planet. What is
- the mass of the brass ball on the Earth and on the planet, and
- the weight of the brass ball on the Earth and on the planet?
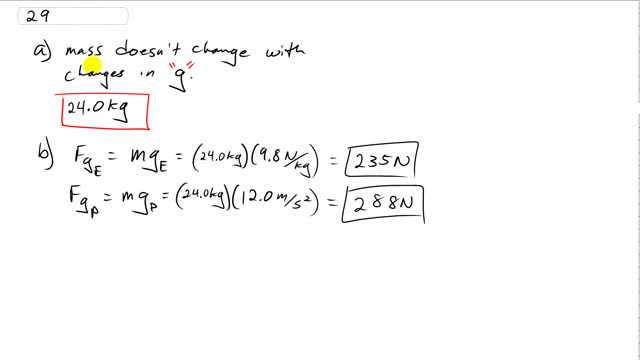
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. Part (a) here is a trick question because mass doesn't change with changes in gravitational field strength, or acceleration due to gravity. The brass ball still has a mass of 24 kilograms on the other planet, just as it does anywhere. The force of gravity, on the other hand, does change; force of gravity on Earth is 24 kilograms times the Earth's gravitational field strength of 9.8 newtons per kilogram, which gives 235 newtons. And on the planet, the force of gravity is gonna be 24 kilograms times 12 meters per second squared which is 288 newtons. And if you are watching closely, you will notice I chose different units in both those cases; either one is fine. I think using newtons per kilogram makes a little bit more sense here because you can see the kilograms cancel and you are left with newtons. But either way, works out and you know that's the case because force is mass times acceleration and so this is Newton's second law and if you divide both sides by m, you can see that acceleration, which has units of meters per second squared, can be thought of as force divided by mass. So we have meters per second squared, on the left side here, for the units, and we have newtons of, which is force divided by kilograms, on the right hand side. They are equivalent; you can interchange them.