Every few hundred years most of the planets line up on the same side of the Sun. Calculate the total force on the Earth due to Venus, Jupiter, and Saturn, assuming all four planets are in a line, Fig. 5–44. The masses are $m_\textrm{V} = 0.815 \; m_\textrm{E}$, $m_\textrm{J} = 318 \; m_\textrm{E}$, $m_\textrm{Sat} = 95.1 \; m_\textrm{E}$, and the mean distances of the four planets from the Sun are 108, 150, 778, and 1430 million km. What fraction of the Sun’s force on the Earth is this?

VIDEO TRANSCRIPT

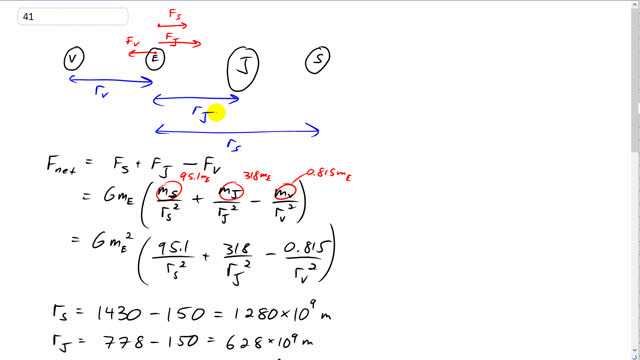
This is Giancoli Answers with Mr. Dychko. So, we have Venus, Earth, Jupiter and Saturn, all lined up along a line and we need to know what the distances are between the Earth and each of these planets, in order to calculate the forces between them. So, the net force is gonna be the force due to Saturn to the right, positive, and then Jupiter to the right. And then also minus the force due to Venus to the left. And that's gonna be capital G times mass of the Earth multiplied by the mass of the Saturn divided by distance to Saturn squared plus the same factor and I have just factored it out here, times mass of Jupiter divided by distance to Jupiter squared and then minus mass of Venus divided by distance to Venus squared. And we are told that the mass of Saturn is 91.5 times the mass of the Earth; mass of Jupiter is 318 times mass of the Earth and Venus is 0.815 times mass of the Earth. And so this, mass of the Earth, is a common factor that can be factored out. This mass of the Earth gets factored out here and becomes mass of the Earth squared. And then we leave the factors by which the planet masses are different there in the numerators and now we have to figure out, what the different distances are. So, the Earth is 150 million kilometers away from the Sun and we know that Saturn is 1430 million miles away from the Sun, or sorry, kilometers away from the Sun. And so take the difference and you get the difference from the Saturn to the Earth. And same story with Jupiter; Jupiter's distance from the Sun minus Earth's distance from the Sun gives you the distance from Jupiter to the Earth. And then we have distance from Earth to the Sun minus distance from Venus to the Sun to get the distance between Earth and Venus. And then substitute all these numbers in; you have, capital G—universal gravitational constant—times mass of the Earth squared times the factor by which Saturn is different from the mass of the Earth and then distance to Saturn squared plus Jupiter's relative mass to the Earth divided by distance from Earth to Jupiter squared and same is the idea with Venus. And you get a net force of 9.597 times 10 to the 17 newtons, away from the Sun. And we have to figure out by what fraction of the Sun's force on the Earth is this. So, we find the force on the Earth due to the Sun. So, we have capital G times mass of the Earth times mass of the Sun divided by the distance from the Earth to the Sun squared and we get 3.547 times 10 to the 22 newtons. So, we take this net force, due to the planet alignment, divided by the force exerted by the Sun on the Earth and we get 2.7 times 10 to the minus 5 is the factor by which they are different. So, the net force is way smaller; it's 27 millionths of the size of the force on the Earth due to the Sun.