
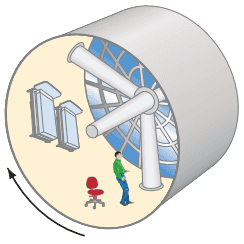
At what rate must a cylindrical spaceship rotate if occupants are to experience simulated gravity of 0.70 g? Assume the spaceship’s diameter is 32 m, and give your answer as the time needed for one revolution. (See Question 9, Fig 5–33.)
In order to watch this solution you need to have a subscription.
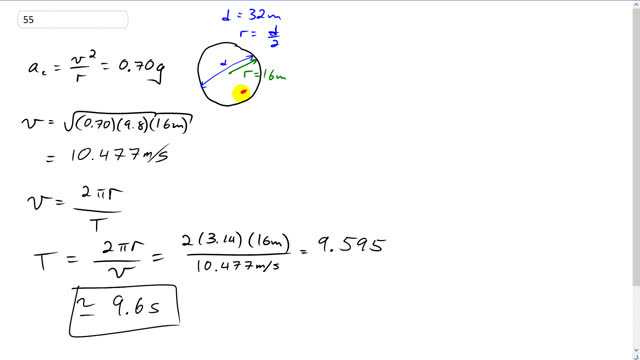
This is Giancoli Answers with Mr. Dychko. With a diameter of 32 meters for this cylindrical spaceship, it has a radius of 16 meters, half the diameter. And some astronaut will be standing here on the edge, say, and they are gonna experience a centripetal acceleration of 0.7 g's; so it's simulated gravity. And that centripetal acceleration will be their tangental velocity squared and divided by the radius of the spaceship. And we can solve this for v, and we'll multiply both sides by r and then take the square root of both sides and we get, v equals square root 0.7g times r and I have put in numbers down here; and that gives square root of 0.70 times 9.8 times 16 meters that gives 10.477 meters per second. So point on the edge of the spaceship has to be traveling with that tangental velocity, 10.77 meters per second. And then knowing that, we can figure out how long it will take to do a full rotation. coz we were told to express our answer as a period; the time for one revolution, in other words. So we have this formula for a period; we know that speed of a point, on the edge of a circle, is gonna be a full circumference, 2πr divided by the time it takes to do one full rotation and then we can solve this for T; multiply both sides by T and divide by r or v, I should say. Multiply by T, divide by v and you get, T equals 2πr over v and that's 2 times pi times 16 meters divided by this speed, 10.477 meters per second, and it'll take 9.6 seconds to do one full revolution, in order to have, simulated gravity of 0.70 g's.