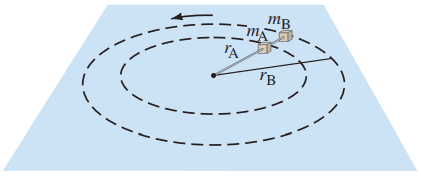
Two blocks, with masses $m_A$ and $m_B$, are connected to each other and to a central post by thin rods as shown in Fig. 5–41. The blocks revolve about the post at the same frequency f (revolutions per second) on a frictionless horizontal surface at distances $r_A$ and $r_B$ from the post. Derive an algebraic expression for the tension in each rod.

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. Here are the horizontal forces shown on the two blocks. I haven't bothered to write the normal force of the gravity because there's no friction involved here so they are not gonna be important. So, we are just dealing with the radial forces here. And then we have the center of the circle somewhere over here. And there's some force of tension on block A pulling it towards the center to make it accelerate in a circle. And then there's this force on block A due to block B in this force on block B due to block A. They are Newton's third law pairs and they are equal magnitudes and we'll just call that force tension on block B. And we'll write Newton's second law for each of the blocks; for block A, we have force tension A is positive because its towards the center and we'll go minus the force of tension block B which is pulling it out and then that equals the net force which is mass times acceleration and the acceleration for block A is the speed of block A—the tangental speed,— squared divided by the radius of the path for A. And Newton's second law for block B is this single force, the tension force on block B which equals its mass times the speed of block B squared divided by the radius of curvature for block B. Now, we can substitute for the speeds by using the frequency that we are given. We know that we want an algebraic expression with the letter f in it because we are given the frequency so we know that speed is gonna be the circumference divided by the period, the time it takes to do one full revolution. So that's 2πr over capital T. And frequency is the reciprocal of period so whenever we have 1 over T, as we do here, we can instead multiply by f So, we have speed is 2πrf in general and then we'll put a subscript A or B on it depending on which formula we substitute into. Let's do the block B first. So, it's gonna have mass B; the tension on block B is mass B times the speed, which is now 2πr times f that's r B in this case and the f doesn't need a subscript because both blocks will have the same number of revolutions per minute; they have the same frequency of their rotation, or revolution I guess. Square that speed, divide by the radius for block B and we have 4π squared the r B squared on top cancels with one of the r B's on the bottom leaving us with r B to the power of 1 on top and the frequency is squared and there we have it! That's the tension force required to keep block B going in the circle, 4π squared mass of block B times the radius for block B times the frequency squared. Now, for block A, we can substitute into this formula and we are gonna substitute for the tension of block B by putting our result there and then equals mass times speed of A using this formula for speed and that's gonna be r A in this case so 2π times r A f squared, divided by r A and and we will have we'll have this turn into 4π squared r A to the power of 1 because r A squared divided by r A is gonna be r A to the power of 1. And the frequency gets squared so this whole thing here is that and then we move this term to the right-hand side, which makes it positive and let's just copy it there. And then we'll factor out the 4π squared f squared f squared there from both terms and we end up with our result here. So that's 4π squared f squared times bracket r A times M A plus radius B times mass B.