
A space shuttle releases a satellite into a circular orbit 780 km above the Earth. How fast must the shuttle be moving (relative to Earth’s center) when the release occurs?
In order to watch this solution you need to have a subscription.
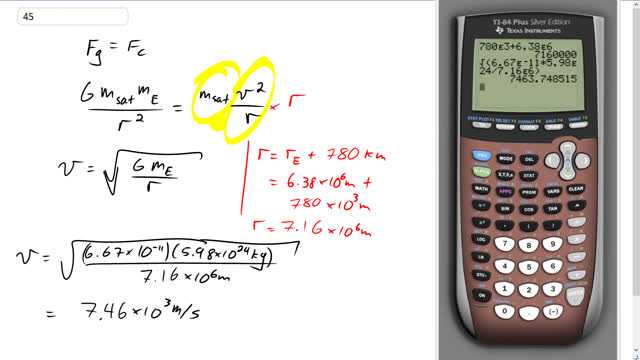
This is Giancoli Answers with Mr. Dychko. The force of gravity is providing a centripetal force for the satellite when it's in orbit. So the centripetal force is mass times centripetal acceleration; so that's m v squared over r and since it's gravity, it's also G— mass of the satellite— mass of the Earth divided by distance to the Earth's center, squared. And we can multiply both sides by r and then that cancels one of the r's here, then take the square root of both sides and canceling mass of the satellite, we get the speed that the satellite needs to have, is the square root of G mass of the Earth divided by r. So r is the radius of the Earth plus 780 kilometers above the Earth's surface. So that's 6.38 times 10 to the 6 meters— radius of the Earth—plus 780 times 10 to the 3 meters which is 7.16 times 10 to the 6 meters, from the center of the Earth. So v is gonna be square root of 6.67 times 10 to the minus 11 times—mass of the Earth—5.98 times 10 to the 24 kilograms divided by 7.16 times 10 to the 6 meters, and we get 7.46 times 10 to the 3 meters per second is how fast it needs to go, which is, times 3.6, which is about 27,000 kilometers per hour; that's pretty fast.