GiancoliAnswers

You are here

  4. Problem 53
Select a problem
Question: 

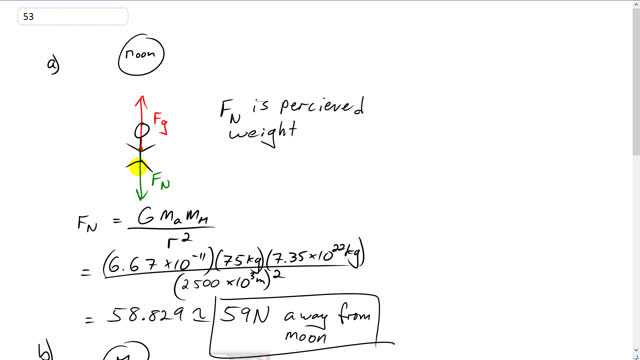
What is the apparent weight of a 75-kg astronaut 2500 km from the center of the Moon in a space vehicle

  1. moving at constant velocity and
  2. accelerating toward the Moon at $1.8 \textrm{ m/s}^2$?

State “direction” in each case.

Source: Giancoli, Douglas C., Physics: Principles with Applications, 7th Edition, 2014.

Quick Answer: 
  1. $59\textrm{ N, away from the moon}$
  2. $76\textrm{ N, toward to moon}$

Giancoli 7th Edition, Chapter 5, Problem 53

(2:59)

Chapter 5, Problem 53 is solved.

View sample solution

Transcript for this Giancoli solution

This is Giancoli Answers with Mr. Dychko. Perceived weight, or apparent weight, is the same as the normal force that the astronaut expriences. We assume that he's in some kind of spacecraft or maybe this, the floor of this spacecraft is applying some normal force on him. Now, there has to be some force in order for him to be going at constant speed because there has to be something to compensate for the gravitational pull of the moon. If there was no normal force, he'd be accelerating towards the moon. But we are told that he's going at constant velocity so there must be some other force, which we will label F N. F N equals F g because of the constant velocity. And so, F N is G mass of the astronaut times mass of the moon divided by distance to the center of the moon squared. So, it's 6.67 times 10 to the minus 11 times 75 kilograms times mass of the moon divided by 2500 times 10 to the 3 meters, squared and that's 59 newtons and so that's gonna be away from the moon, as shown in the diagram. And then, in part (b), we have F g; we'll take positive to be towards the moon. So, we have F g positive minus F N because F N is directed away from the moon in our picture anyway, equals mass times acceleration. This is a net force so net force is always ma. We'll take the mass acceleration term to the left, making a minus. And then take the normal force turn to the right, making a positive. Switch the sides around and we get normal force is gravity minus M a. We can factor M a out of both, this term and it's gonna appear in this gravity term. So, we'll have M a times bracket gravitational constant times mass of the moon divided by distance to the center of the moon squared minus the acceleration. And that's 75 kilograms times G times mass of the moon divided by distance to the center of the moon squared. And then minus this positive 1.8 meters per second squared because the acceleration is towards the moon. This minus stays there though as a result of this algebra we did, by moving the M a term to the other side. And we get negative 76 newtons; and this negative means that that the normal force is in the opposite direction to the way we have drawn it. So, I put a minus in front of it to indicate that it was away from the moon. But, getting a negative result means that it is in fact, pointing towards the moon. A bit confusing I guess since I said position direction is towards the moon. But, in doing that, that's resulted in this minus sign in my original equation. And so. And as we carry on, if we end up with a negative answer, that means whatever assumption we made in the original equation, was, is now actually the opposite. So, there. 76 newtons towards the moon is the perceived, apparent weight.