
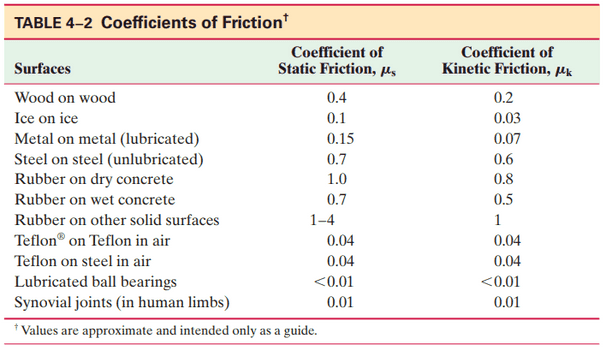
Highway curves are marked with a suggested speed. If this speed is based on what would be safe in wet weather, estimate the radius of curvature for an unbanked curve marked 50 km/h. Use Table 4–2 (coefficients of friction).
In order to watch this solution you need to have a subscription.
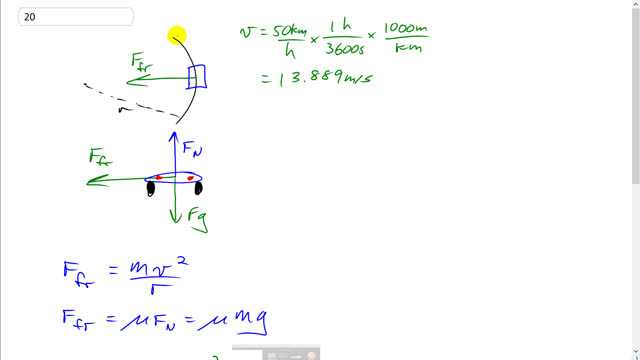
This is Giancoli Answers with Mr. Dychko. Here's a top-down view of the car going around the curve. There's a friction force directed towards the center of the radius of curvature of this turn and this turn has a radius r. And the car's going at 50 kilometers an hour, which we convert into meter per second; multiplying by 1 hour for every 3600 seconds. And the hours cancel and then times by a 1000 meters per kilometer; then you get meters per second. That's 13.889 meters per second; 50 divided by 3.6, in other words. Here's a behind-the-car view, a rear view and these are the taillights; these red dots and you can see the tyres there too. We have a normal force upwards and gravity down and they are equal size because there's no acceleration, vertically. And there's a single force, horizontally, friction force to the left because that's the direction the car is accelerating; it's going forward but it's also gonna accelerate to the left. So, the friction force is the centripetal force that equals mass times this car's acceleration. And the acceleration since it's going in a circle at constant speed, the acceleration is v squared over r and friction force, also we know, is the coefficient of friction times normal force but the normal force upwards equals the gravity down. Since there's no vertical acceleration so we can write mg in place of gravity for the normal force. And, then we'll say that this one equals friction and this one also equals friction so that means these equal each other. So, µmg equals m v squared over r. And then we'll solve for r by multiplying both sides by r and dividing both sides by g and the g's cancel on the left and we'll also divide by µ and the µ's cancel on the left leaving us with r on the left. The m's, we are also dividing both sides by m, the m's cancel too. So, what we are left with is r equals v squared over µg. So that's 13.889 meters per second and we square that, divided by 0.7, which is the coefficient of static friction for rubber and wet concrete, because the car is not skidding so it's considered static friction even though the wheels are rotating. More specifically, it's more precisely, it's rolling friction is what it should be but static friction is close enough. And so we use 0.7; there's only one significant figure on that because it's just an estimate, you know, depends on the brand of tyre, I suppose and so on, or how wet the concrete is. And so that's why we are only gonna have one significant figure in our radius of curvature, this 28.1197 is gonna get rounded to 30 meters, is the minimum radius of curvature the turn could have, with a posted speed of 50 kilometers an hour, maximum.