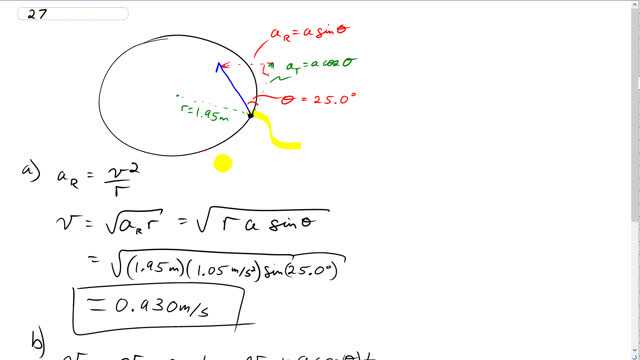
A particle revolves in a horizontal circle of radius 1.95 m. At a particular instant, its acceleration is $1.05 \textrm{ m/s}^2$, in a direction that makes an angle of $25.0 ^\circ$ to its direction of motion. Determine its speed

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. The acceleration of this particle is at an angle of 25 degrees with the direction of motion and the direction of motion of a particle going in a circle is always tangental to the circle. So that means we can take this acceleration, divide it into tangental components by taking the cosine of this angle times the acceleration and we can also find the radial component. And the radius of the circle is 1.95 meters and let's start by finding the the tangental speed, well the only speed, of this thing by using the radial acceleration is speed squared divided by r. So, we'll multiply both sides by r and then take the square root of both sides and we get, v is square root of radial acceleration times r. So radial acceleration is acceleration times sin theta because it's the opposite leg of this right triangle; it doesn't really look like a right triangle, the way I have drawn it, but I had to make these lines pretty long, in order to illustrate them properly. But, you can make the lines really really short, in which case, this would point directly at the center, at a 90 degree angle. So we have square root of 1.95 meters times 1.05 meters per second squared times sin of 25 degrees gives 0.930 meters per second, must be the speed of this thing. And then sometime later, it's gonna have a different speed because it's accelerating tangentally as well and the tangental acceleration can be found with a times cos theta because that's the adjacent leg of this right triangle so we use cosine of 25 degrees times the resultant acceleration to get this component, this tangental. So, we have the 0.930 meters per second that it starts with times by the acceleration 1.05 meters per second squared times cos 25 to get the tangental component of the acceleration multiply by 2 seconds later gives 2.83 meters per second.