
Use Kepler’s laws and the period of the Moon (27.4 d) to determine the period of an artificial satellite orbiting very near the Earth’s surface.
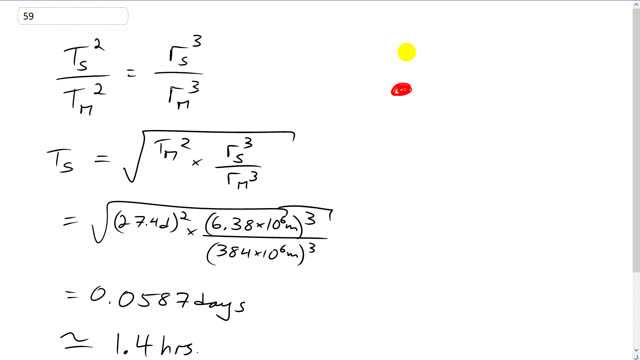
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. Kepler's laws don't always have to involve the sun; we can use any body as the central source for gravity, or the thing that something else is orbiting around, in other words. In this case, the Earth is what we have as the focus for the orbit; the focus of the ellipse in which the orbit is happening. So we have the moon going around the Earth and we have this satellite, in a near Earth orbit, which is at a distance, basically equal to the radius of the Earth say. And the square of the period of the satellite divided by the square of the period of the moon is gonna equal the cube of the satellite's orbital radius divided by the cube of the moon's orbital radius. And we can solve for the period of the satellite's orbit by multiplying both sides by period of moon's orbit squared and then take the square root of both sides and so we have square root of 27.4 days squared and because we kept the units in days, that means we know in our final answer, we are gonna have days. And that's times by the radius of the Earth which is basically the orbital radius of the satellite, 6.38 times 10 to the 6 meters, and we cube that and divide by 384 times 10 to the 6 meters cubed; that's the distance from the moon to the Earth's center. And that is 0.587 days, which is about 1.4 hours, for this near Earth satellite to complete one orbit. And it would be interesting to compare that to what you would get by using a centripetal force and gravity; you can go G mass of the satellite mass of the Earth divided by the Earth's radius squared and that equals m v squared over r. See what you get there; express v in terms of period and see if you get 1.4 hours there, and you should.