
If you doubled the mass and tripled the radius of a planet, by what factor would g at its surface change?
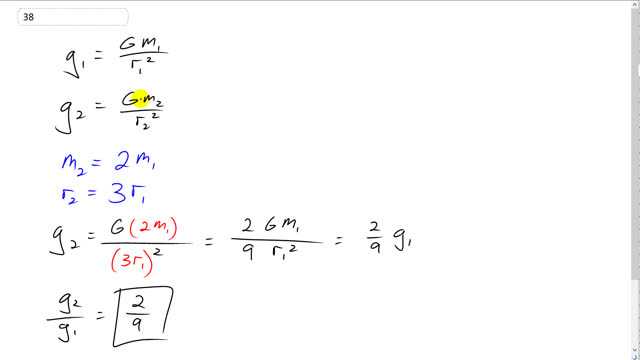
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. In the first case, acceleration due to gravity will be capital G times some original mass divided by some original radius squared. And then in the second case, we have a different mass and a different radius, and we are told that the mass two is twice mass one, with double the mass, and the radius in the second case is triple the radius in the first case so 3 times r 1. So we make substitutions for each of these in the second case for acceleration due to gravity. So we have capital G times 2 m 1 instead of m 2 and we have 3 r 1 instead of r 2. By the way, I should have a square there, that's better. This 3 on the bottom becomes 9 because it gets squared and so we have two-ninths times capital G m 1 over r 1 squared and this whole thing is the acceleration due to gravity, in the first case, before you doubled the mass and tripled the radius. So that means that the acceleration due to gravity changes by a factor of two-ninths, in the second case, after you double the mass and triple the radius.