
The comet Hale–Bopp has an orbital period of 2400 years.
- What is its mean distance from the Sun?
- At its closest approach, the comet is about 1.0 AU from the Sun (1 AU = distance from Earth to the Sun). What is the farthest distance?
- What is the ratio of the speed at the closest point to the speed at the farthest point?
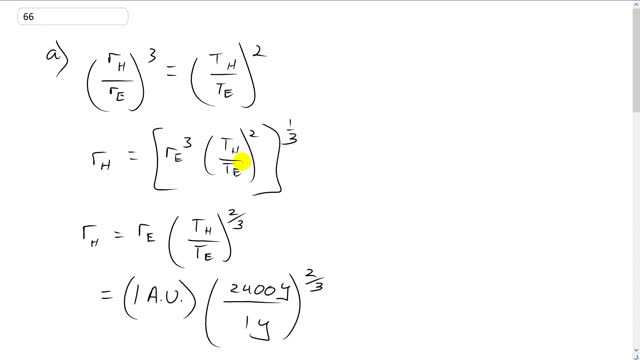
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. The orbital radius of this Hale-Bopp comet divided by the orbital radius of Earth cubed equals the ratio of their periods squared -- that's Kepler's third law. And multiply both sides by Earth's orbital radius cubed and then take the cube root of both sides which is the same as exponent one-third both sides. The Hale-Bopp orbital radius cubed exponent one-third makes the power of 1. And on the right hand side, we end up with the ratio of the periods to the power of 2 over 3 and then here's the orbital radius of the Earth. So, orbital radius of the Earth is 1 astronomical unit times 2400 years for Hale-Bopp's orbital period divided by 1 year for Earth, all to the power of two-thirds gives about a 180 astronomical units must be the mean orbital distance for the Hale-Bopp comet. Now, we are told that the closest distance is about 1 astronomical unit and the furthest Hale-Bopp distance is what we have to find. So we take this mean, which we just found, 180 and that mean equals the closest plus the furthest divided by 2 -- that's the average. And then, we'll multiply both sides by 2 and then subtract r closest and we get r furthest is the 2 times the mean minus the closest. So we get about 360 astronomical units is the furthest distance from the Sun to the Hale-Bopp comet. And then part (c), we're gonna use the second law, I believe, for Kepler where he says that the area that's of this sector during some period of time at any distance equals the area of the sector carved out by the motion of the planet or asteroid or comet for same period of time at any other point along the orbit. So this shaded yellow area equals the shaded blue area. Now dealing with such, we can choose what period of time we want to consider here because it's for any period of time. And we can choose it for a really short period of time and by doing that, we can approximate the area of the sector to be the area of a triangle. So, area of a triangle is the base times the height. But the height, you know, when we choose a really short period of time; this little leg of the triangle you can imagine that it gets really close to the other one and they are and when it gets really really small, the height of this triangle is essentially gonna be the same length as the sides of the triangle. So choosing a really short period of time makes that true. And also this distance along the ellipse, along this curve is essentially gonna be the same as the linear base of this triangle. So this red line here when we choose a really short period of time because when you zoom in, on this curve, the curve will essentially become like a straight line just like the surface of the Earth looks like it's flat because you know, we have a very small zoomed in perspective on the planet but when you go out into space, you can see the curvature and so on. So, it's a question of perspective here and when you choose a really short period of time, you are able to make this a really small sector and the base and the height of of the triangle is gonna equal the area of the sector. So, the base is gonna be the speed times time and that's why we have vt here in place of b. And then the height is gonna be the distance from the Sun. And so the area when you are at a minimum distance, that's this blue area here, is gonna equal the area at this maximum distance -- that's Kepler's law. And so, v, the speed at this minimum distance multiplied by whatever arbitrary amount of time we have here, which was really short in order to use this approximation as base times height for the area of the sector times the distance, minimum distance to the Sun, equals v max t times r max. And so divide both sides by v max, cancel the time; you know, we chose a really short period of time in order to make our approximations and it turns out that time is otherwise irrelevant, it just cancels anyways so that's nice, which means we can choose it to be what we want And when we have r max divided by r min so divide by r min on both sides. And so v max's cancel here, r min's cancel here and we have v min over v max equals r max over r min. So the speed at the minimum distance divided by speed at the maximum distance is the maximum orbital distance, which is, or maximum distance from the Sun is 357 astronomical units divided by the minimum distance which is 1 Earth orbital radius, which is 1 astronomical unit and we get about 360 as the ratio of the speeds at the minimum distance to the maximum distance. So, it's going much faster when it's close to the Sun than it is farthest from the Sun; it is going 360 times faster when it's close to the Sun compared to when it's far from the Sun.