
Giancoli's Physics: Principles with Applications, 7th Edition
5
Circular Motion; Gravitation
Change chapter5-1 to 5-3: Uniform Circular Motion
5-4: Nonuniform Circular Motion
5-5 and 5-6: Law of Universal Gravitation
5-7: Satellites and Weightlessness
5-8: Kepler's Laws
Question by Giancoli, Douglas C., Physics: Principles with Applications, 7th Ed., ©2014, Reprinted by permission of Pearson Education Inc., New York.
Problem 33
Q
Calculate the acceleration due to gravity on the Moon, which has radius and mass .
A
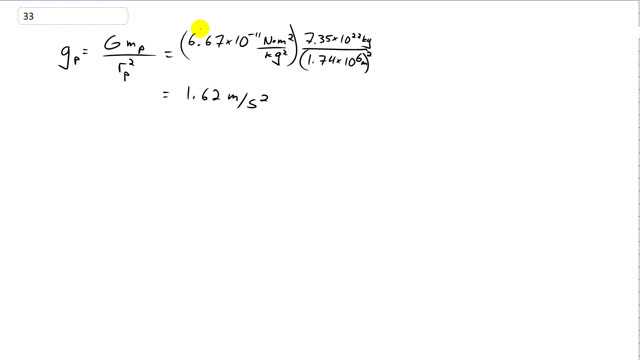
In order to watch this solution you need to have a subscription.
VIDEO TRANSCRIPT
This is Giancoli Answers with Mr. Dychko. Acceleration due to gravity on any planet or moon is the universal gravitational constant, capital G, times the mass of the planet divided by the radius of the planet squared. So in this case, we'll use the mass of the moon—7.35 times 10 to the 22 kilograms and divide that by the radius of the moon— 1.74 times 10 to the 6 meters and square that multiplied by the gravitational constant— 6.67 times 10 to the negative 11 newton meter squared per kilogram squared to get the acceleration due to the gravity on the moon of 1.62 meters per second squared.
Giancoli Answers, including solutions and videos, is copyright © 2009-2024 Shaun Dychko, Vancouver, BC, Canada. Giancoli Answers is not affiliated with the textbook publisher. Book covers, titles, and author names appear for reference purposes only and are the property of their respective owners. Giancoli Answers is your best source for the 7th and 6th edition Giancoli physics solutions.