
Determine the mass of the Earth from the known period and distance of the Moon.
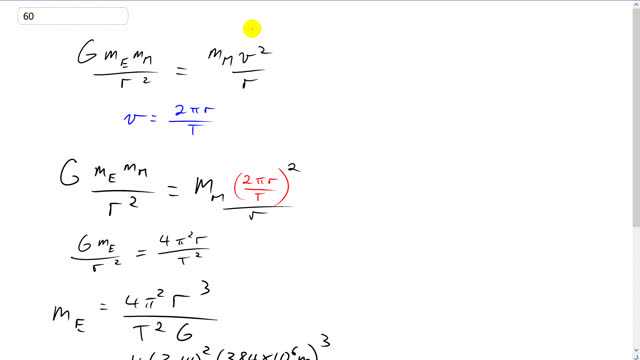
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. The gravitational force on the moon is G times mass of the Earth times mass of the moon divided by distance from the center of the Earth to the center of the moon squared. And that gravitational force is the centripetal force and so it equals mass times acceleration; it's the net force. And acceleration in this case since it's going around in a circle, this moon is orbiting in a circle you assume, the centripetal acceleration is v squared over r. And, v, we can express in terms of period because that's the information we are given; 27.4 days is the period of the Earth's orbit. So, we should write v, in terms of period, as 2πr over T; that's the circumference of the circle the orbit's revolving in divided by the time it takes to do one full circle, period. And then substitute that in for v. So v is rewritten as 2πr over T here and that gets squared, and divide by r, you end up with 4π squared and it would be r squared but then it's divided by r so that just makes r to the power of 1 and divide by T squared; mass of the moon cancels on both sides and we have G M E over r squared, otherwise copied on the left, and we can solve for the mass of the Earth by multiplying both sides by r squared and dividing by universal gravitational constant, capital G, and you get, mass of the Earth must be 4 π squared r cubed over T squared G. So that's 4 times 3.14 squared times 384 times 10 to the 6 meters, which is the distance from the center of the Earth to the center of the moon, cubed, divided by gravitational constant, 6.67 times 10 to the minus 11 and then times by the the period squared, and the period we'll have to write in mks units; we'll have to write it in seconds, in order to match with with the other units that are being used in this formula. So that's 27.4 days times 24 hours per day times 3600 seconds per hour giving us seconds in the end. And square that period and you get 5.97 times 10 to the 24 kilograms, must be the mass of the Earth.