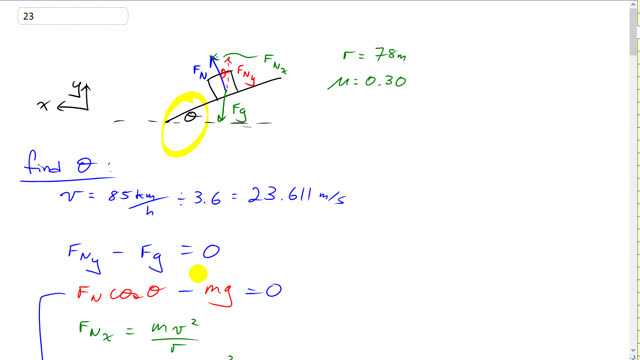
A curve of radius 78 m is banked for a design speed of 85 km/h. If the coefficient of static friction is 0.30 (wet pavement), at what range of speeds can a car safely make the curve? [Hint: Consider the direction of the friction force when the car goes too slow or too fast.]

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. Our first job for this long question is to figure out what is this banking angle. I guess one of the examples, in the textbook, gives a formula for calculating it but I'm gonna do it from scratch here. We have a speed of 85 kilometers per hour is the designed speed for the curve and that's 23.611 meters per second when you divide by 3.6 to convert it. And, in the y-direction, we have the y-component of this normal force minus gravity; all that equals zero because well, that's the net force vertically and so it equals mass times acceleration but there is no acceleration vertically and so we just have zero. And then we can substitute for each of these things and write F N y is normal force times cos Θ because it's the adjacent leg of this triangle and then minus mg for the weight. And then we'll consider the x-direction and we can see that the centripetal force is provided by the x-component of the normal force and that's the opposite leg of this triangle so we use F N times sin Θ to get that. And in the x-direction, it is accelerating so there's mass times centripetal acceleration and centripetal acceleration is v squared over r. Or we have chosen our x-axis to be straight horizontal in the direction of acceleration and y-axis is straight up and down. Then we'll rewrite this equation solving it for F N by moving mg to the right-hand side which makes it positive and then divide both sides by cos Θ. And we get normal force is mg over cos Θ and then we substitute that result into we'll substitute this result into this equation here for F N. And so we have mg over cos Θ times sin Θ equals mv squared over r. sin Θ divided by cos Θ is a trigonometric identity equaling tan Θ. And the m's cancel on both sides and so we have gtan Θ equals v squared over r and divide both sides by g and we get tan Θ is v squared over rg. And that means Θ is the inverse tangent of this speed squared, 23.611 meters per second and then divide by the radius of curvature of 78 meters and divide by 9.8 meters per second squared to get 36.103 degrees, is the banking angle. And then we consider the range of speeds that this curve could be taken knowing the coefficient of friction is 0.3 and we'll consider the fastest speed first. And, in that case, we have friction acting down the ramp because there's going to be a need for more centripetal force than the normal force can possibly provide. And so, there's gonna need to be this component provided by friction in that x-direction to make up for what the normal force is on its own lacking. So, these two combine— this x-component of normal force and this x-component of friction— will together make the centripetal force and result in the acceleration that's radial or centripetal. OK So and then we are gonna consider the slowest speed down here where friction is acting up the ramp because the x-component of the normal force will be too much centripetal force. The car is going slow enough that it's centripetal acceleration, it would have too much centripetal acceleration with this normal force and so we'll have to reduce the centripetal force by having a component of friction acting away from the center of curvature— that's one way to look at it. Another way to look at it is that this car—even if it was just standing still— would go on its down the ramp and so you can imagine that as it's going slow, it's going to need some friction up the ramp to keep it from sliding down. So, either way you look at it, you have friction going this way when the car's going slow. But first, let's look at it going fast. So, in the y-direction, Newton's second law, we write down all the up forces minus all the down forces equals the acceleration vertically—of which there's none—so we have zero there. So, we have normal force y-component upwards— that's positive—and then minus the component of friction, which is down and then minus gravity, which is entirely down. And substitute for each of these things, we have y-component of normal force is the normal force times cos Θ because it's the adjacent leg of that triangle. And then y-component of friction is friction force times sin Θ because this y-component is the opposite leg of this triangle and then minus mg for gravity. And then substitute for friction force is µ times F N. And that's pretty much as far as we can go with equation 1. We have, well. First of all, we don't have the speed appearing anywhere in that equation so we need an equation with the v because that's what we are solving for and so let's look at the x-direction. So, the x-component of the normal force plus the x-component of friction force are together providing all the forces in the x-direction and those equal mass times acceleration in the x-direction and acceleration in the x-direction is v squared over r. So, we have F N x plus force of friction x equals mv squared over r. And then substituting for each of those; x-component of normal force is normal force times sin Θ because it's the opposite leg of that triangle and then x-component of friction is force of friction times cos Θ because it's the adjacent leg of this triangle and that equals mv squared over r—just copied. And then we have substitution for friction is µF N and otherwise, I copied everything from this next line. And then we're gonna do a look at equation 1 again and think about how we can combine it with equation 2 to solve for v; that's the job here. And there's multiple ways to go about it. It's a mathematics problem at this point; how do we do the algebra to solve this system of simultaneous equations is a fancy way of describing what we are doing here. We have two unknowns and two equations and we have to solve for the unknown that we are interested in, which is v. So, we are not interested in the normal force— that unknown we would like to just disappear. So, we can make that happen by rewriting equation 1 with the normal force factored out and times by cos Θ minus µsin Θ. And then move this mg term to the right-hand side so it equals mg— positive on the right side— and then we write equation 2, as shown here, factoring out F N and it's times sin Θ plus µcos Θ equals mv squared over r. And the next coincidence that if you take equation 2b, and divide it by equation 1b, the F N's will cancel. You could have also done method of substitution which would be to solve one of these equations for the normal force and then substitute that result into the other equation— that would work fine too. So, we have equation 2b, and that's sin Θ plus µcos Θ after you get rid of the F N, divided by cos Θ minus µsin Θ Also, the F N is canceled there and then on the right-hand side, dividing that you have mv squared over r divided by mg; the m's will cancel leaving us with v squared over rg. And then we solve for v. So multiply both sides by rg and then take the square root of both sides and—I also wanna do something else here; just optional but to be really slick, I decided to multiply top and bottom by 1 over cos Θ. You can do anything you want in algebra so long as you don't change the quantity. We're just changing the way things look but we are not changing any values here because we are essentially, multiplying by the number 1; 1 over cos Θ divided by 1 over cos Θ is 1. So, you can always multiply by 1 and what that's gonna do is it's gonna make this sin Θ divided by cos Θ turn into tan Θ and then cos Θ divided by cos Θ will just end up being 1 and so you have only the µ here. And same kind of story on the bottom, we have cos Θ over cos Θ is 1 minus µ times sin Θ over cos Θ which is tan Θ. And then, yes, we have this rg being multiplied by all of it here too and take the square root of both sides because it's v squared and we want to solve for v. So, we have v is then going to be square root of 78 meters times 9.8 meters per second squared times tan 36.103—banking angle— plus 0.3—coefficient of friction— close bracket, divided by 1 minus 0.30 times tan 36.103 and you get 32 meters per second is the maximum speed that you can take this curve. Then consider the slowest speed. So, the picture has friction going up the ramp— as I talked about before— and we are gonna do Newton's second law for each of the x and the y dimensions. So, we have F N y plus force of friction y equals F g. Notice there's F N y plus force of friction y, in this case. The y-component of friction is in the same direction as the y-component of normal force now. That's different than the previous picture where we have the y-component of friction against the normal force y-component. And so together these two components, add up to the total down force, which is gravity, and then we'll make substitutions for each of these things and we'll have normal force times cos Θ which gives a y-component plus friction force times sin Θ gives its y-component equals mg for gravity. And then substitute for friction is µF N and we have the y-direction equation is gonna be normal force times cos Θ plus µF N sin Θ equals mg. Then, considering the x-direction, we have the x-component of the normal force and then minus the x-component of friction. Remember I said before that the x-component of normal force is is more force than needed for the small amount of centripetal force required here since it's going so slow. So, we need to reduce the centripetal force by having this minus, this friction working against the excessive x-component of the normal force and that's what you see here. Put this minus sign there and that total equals the mass times acceleration in the x-direction which is mv squared over r— v squared over r because it's centripetal acceleration. And then we do substitutions for each of these things. F N x is the is the opposite leg of this triangle so we use sin Θ times F N to calculate that. And then force of friction x is the adjacent leg so we use cos Θ times friction to get that. And then copy the mv squared over r there and substitute for force of friction is µ times normal force. And then, factor out the F N from all this and we get equation 2, say. And that's F N times sin Θ minus µcos Θ equals mv squared over r. And then we'll take equation 1 and factor the F N out of it. And we are doing the same sort of trick as we did before where we are aiming to solve for v and we need to change the way these equations look so that we can divide them and get rid of the unknown that we don't care about— which is the normal force. So we have equation 2 divided by equation 1 version b gives us this. So we have sin Θ minus cos Θ is here divided by cos Θ plus µsin Θ and the F N's canceled when we did that division. And then we have mv squared over r divided by mg so that's v squared over rg. and we get this equation when you multiply— same sort of stuff as before—top and bottom by 1 over cos Θ and then multiply both sides by rg and then take the square root of both sides. So, this is the exact same stuff as we had before except instead of a a minus, we had a plus before and instead of a plus on the bottom, we had a minus before. So that's interesting. And that means our calculator work is gonna be simple because we can fire up the calculator and go second function entry and get the same stuff we had before and just change the signs. So, it's a minus on top now and it's a plus on the bottom now. And we get 16.409. So, the range of speeds has to be greater than or equal to, say, 16 meters per second, or, less than or equal to the maximum of 32 meters per second, or you could express that in kilometers per hour. And say that the speed should be— anywhere between— 57 kilometers per hour; although we are making a bit of a intermediate rounding error here because I shouldn't take the 16 and multiply it by 3.6, I should take the 16.409 16.409 times 3.6—and what does round to—that rounds to 59. So between 59 kilometers an hour— that's at a minimum— or, at a maximum, 31.735 times 3.6—at a maximum—you can go 114 kilometers an hour; and with two significant figures, let's call it 110 and there we go! Good job if you followed all the way through all that. That was a tricky question!