
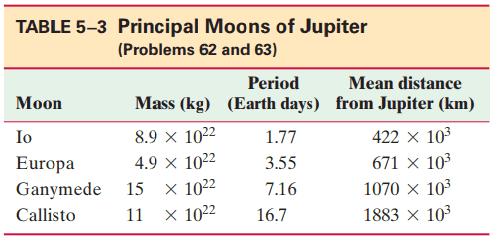
Determine the mean distance from Jupiter for each of Jupiter’s principal moons, using Kepler’s third law. Use the distance of Io and the periods given in Table 5–3. Compare your results to the values in Table 5–3.

In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. The orbital radius of some moon cubed divided by the orbital radius of Io cubed equals the period of some other moon squared divided by the Io's orbital period squared. So we can solve for the distance to some other moon's orbit by solving for r M and we'll multiply both sides by Io's radius of orbit cubed on both sides here and take the cube root of both sides. Now, the cube root of r I cubed is r I and then we have the cube root of period of the moon squared divided by the period of Io squared. And so then we can use this formula for all of three of the other principle moon's of Jupiter. So, we have 422 times 10 to the 3 kilometers times cube root of 3.55 days— orbital period of Europa— squared divided by—the orbital period of Io—1.77 days squared; we can have days here because we know the days are gonna cancel so we don't need to change them into seconds. And since we didn't change the kilometers into meters that means our answer's gonna be in kilometers which is good for comparison because in the table 5-3, we are comparing with kilometers so it's good to have the units the same. Well, we have 6.711 times 10 to the 5 kilometers and in the textbook, we have 671 times 10 to the 3 kilometers and that's pretty much the same. And then for Ganymede, we have the same orbital radius for Io times the cube root of Ganymede's orbital period, squared, divided by Io's orbital period squared and then we get 1071 times 10 to the 3 kilometers which is, compared to 1070 times 10 to the 3 kilometers in the textbook is pretty close. And then when we look at Callisto, we have 16.7 days and that squared divided by 1.77 days— orbital period for Io—squared and then take the square root of that result and then times by the orbital radius of Io and you get 1883 times 10 to the 3 kilometers, which is bang on the same as what we have in the textbook.