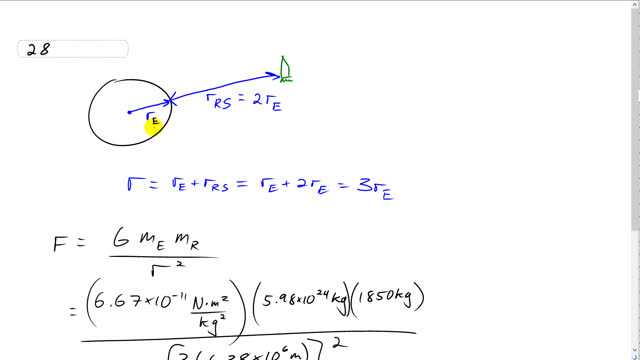
Calculate the force of Earth’s gravity on a spacecraft 2.00 Earth radii above the Earth’s surface if its mass is 1850 kg.

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. The distance from the Earth's surface to the rocket is two times the Earth's radius. And the distance we are interested in is from center of mass to center of mass so the distance from the rocket to the Earth's center of mass is the distance to the Earth's center. The Earth's geometric center will be its center of mass as well because it's a, you know, a sphere of uniform mass distribution, you can assume. So the distance r that we use in this formula, for calculating gravity, is going to be radius of the Earth plus two times the radius of the Earth and that's a total of three Earth radii distance from center to center. So we have the force then is 6.67 times 10 to the minus 11 newton meter squared per kilogram squared times 5.98 times 10 to the 24 kilograms— mass of the Earth— times—mass of the rocket—1850 kilograms divided by 3 times—the Earth's radius— 6.38 times 10 to the 6 meters and we square that result of multiplying by 3 and you end up with three significant figures; the force of 2010 newtons.