
The design of a new road includes a straight stretch that is horizontal and flat but that suddenly dips down a steep hill at . The transition should be rounded with what minimum radius so that cars traveling 95 km/h will not leave the road (Fig. 5–40)?

In order to watch this solution you need to have a subscription.
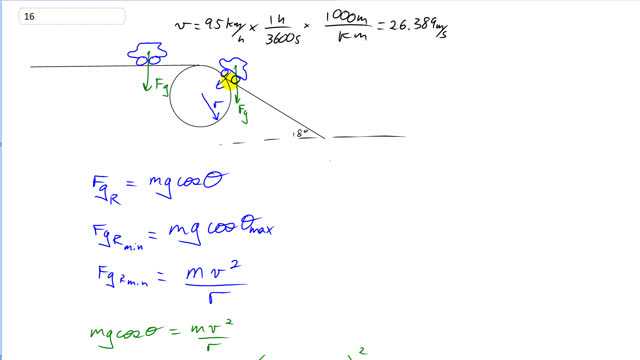
This is Giancoli Answers with Mr. Dychko. This car is initially traveling on a level road and then it approaches this portion of curvature here, as it transitions on to the sloped road, sloped at 18 degrees. And while it's going over this curve, there's a centripetal force that's making it have this acceleration along the circle and that centripetal force is provided by gravity but it's not just gonna be mg, instead it's gonna be whatever component of gravity is directed towards the center of the circle. And that changes as it passes through the circle. So, when the car is just up here, gravity is straight down here say, and at the very beginning of the circle, it will still be straight down and it will be towards center of the circle, probably. And I mean the way I have drawn it, it will be but depending on how big the circle is, I guess. But at some point, as it goes along this curve, gravity is no longer directed towards the center of the circle and so this component of it here is going to provide the centripetal force. And we find that component by knowing that this angle up in that corner is; that's also 18 degrees. And so this component of gravity, the radial component I have called it, F g R is mg times cos Θ since it's the adjacent leg of this triangle here, if you imagine here's the component of gravity that's accelerating along the ramp now and drawn in red there but you know, never mind that; it's this part here, the radial part that we are concerned with. So, force of gravity that's radial is mgcos Θ. And that's gonna be changing as the car passes around the circle as that angle Θ changes until it finally gets to a maximum of 18 degrees. And so, the smallest centripetal force it will experience along this circle is gonna be when it gets to this point at the end of the circle when it's finally on this maximum angle of 18 degrees. So, the minimum radial force will be mg times cos Θ max, which is 18. And, at that point, well, at all points really, the radial component of gravity has to be mv squared over r or mass times acceleration; acceleration being centripetal acceleration so it's v squared over r. And then, we can say that this equals that because they are both equal to this. So, we are gonna solve for r now and divide both sides by m, multiply both sides by r and divide both sides by gcos Θ and gcos Θ cancels on the left side leaving us with r there and then we have v squared over g times cos Θ on the right. So, we have converted the speed 95 kilometers per hour into meters per second by dividing by 3.6 which is 26.389 meters per second and then divide by 9.8 meters per second squared, g, and then divide by cos 18. So that gives 75 meters is the radius needed to prevent the car from from lifting off the ground. And I guess I should also mention that that condition also means that the normal force is zero so that's why you don't see any other forces on the car. This is the case where it's just about to leave the ground is that point where the normal force just begins to equal zero.